Математика \ Дискретная математика

Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 4

   Х - множество сотрудников НГТУ; Y - множество учебных групп;
пусть (x, y) Î Q тогда и только тогда, когда сотрудник х ведет занятия в группе y, т.е. Q = {(x, y)|xÎХ, yÎY и х ведет занятия в y}. Пр1Q Ì X - множество сотрудников НГТУ, участвующих в учебном процессе (в этой записи учтено, что не все сотрудники НГТУ участвуют в учебном процессе), Пр2Q = Y, так как в каждой учебной группе кто-то из сотрудников ведет занятия.

  В этом примере Q устанавливает некоторое соответствие между множеством сотрудников НГТУ и множеством учебных групп.

Пример 1.2.

   F={f(x)} - множество функций действительного переменного f(x);
R={r} - множество действительных чисел.

   Пусть     
           

  В этом примере J ставит в соответствие действительные числа функциям действительного переменного.

  Пр1J Ì F, так как указанный в определении интеграл существует не для любой функции действительного переменного.

  Пр2J = R, так как любое действительное число может быть значением данного интеграла.


1.4.2. Способы задания соответствий

   Для задания соответствия нужно, очевидно, определить все три множества Х, Y и Q.

   Множества Х, Y и Q задаются так же, как и любые другие множества, например, перечислением их элементов или заданием характеристического свойства, множество Q при конечном количестве его элементов может быть задано также в виде матрицы или графически.

Пример 1.3.

Х={Ренин, Кошкин, Хоменко};

Y={ВИ-91, ВИ-81, АС-812, АС-813, АС-814}

Q={(x, y)|xÎХ, yÎY и x ведет занятия в группе y}

   Так как число элементов во множествах Х и Y конечно, то это соответствие можно задать и перечислением элементов:

   Q={(Ренин, ВИ-91), (Ренин, ВИ-81), (Ренин, АС-812), (Ренин, АС-813), (Ренин, АС-814), (Кошкин, АС-812), (Кошкин, АС-813), (Кошкин, АС-814), (Хоменко, ВИ-81)}

1.4.2.1. Матричный способ задания

   Для задания соответствия строится матрица, каждой строке которой ставится в соответствие ровно один элемент области отправления Х, а каждому столбцу – элемент области прибытия Y. На пересечении строки и столбца ставится 1, если соответствующие им элементы образуют пару, принадлежащую соответствию Q, в противном случае ставится 0.

Пример 1.4.

   Соответствие из предыдущего примера в матричной форме имеет вид:

ВИ-91

ВИ-81

АС-812

АС-813

АС-814

M(Q) =

Ренин

1

1

1

1

1

Кошкин

0

0

1

1

1

Хоменко

0

1

0

0

0

1.4.2.2. Графический способ задания

   Для задания соответствия Q каждому элементу множеств X и Y ставится в соответствие произвольная точка на плоскости. Если пара (x, y)ÎQ, то элементы x и y соединяются стрелкой, идущей от х к y. Соответствие из предыдущего примера в этом случае имеет вид:

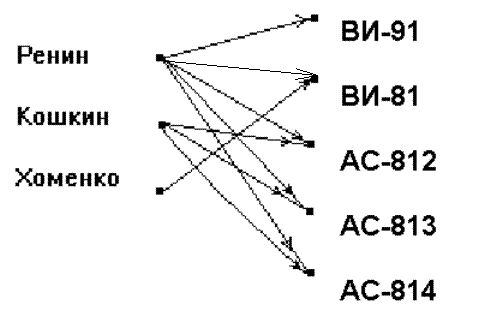
1.4.3. Операции над соответствиями

   Так как соответствия являются множествами, то над ними можно выполнять все те операции, что и над обычными множествами, в частности объединение и пересечение. Кроме того, имеются специфические для соответствий операции - симметризация и композиция.

1.4.3.1. Объединение соответствий

   Пусть q = <X,Y,Q> и s = <U,V,S> - два соответствия.

   Соответствие p = <Z,W,P> будет объединением соответствий q и s
(p = q s), если Z=X U, W=Y V и P=Q S.

1.4.3.2. Пересечение соответствий

   Пусть q = <X,Y,Q> и s = <U,V,S> - два соответствия.

   Соответствие p = <Z,W,P> будет пересечением соответствий q и s
(p = q s), если Z=X U, W=Y V и P=Q S.

1.4.3.3. Симметризация соответствий

   Пусть q = <X,Y,Q> - некоторое соответствие. Соответствием, обратным соответствию q, называется соответствие q-1 = (Y, X, Q-1), в котором Q-1ÍY´X и пара (y, x)ÎQ-1 тогда и только тогда, когда пара (x, y) ÎQ.

   Операция получения обратного соответствия называется симметризацией.

   Если соответствие задано перечислением входящих в него пар, то для получения обратного соответствия нужно просто переставить местами элементы в каждой паре.

Скачать файл