Обычно этим правилом пользуются, если множество всех расстановок, которые необходимо сосчитать, удается разбить на непересекающиеся подмножества расстановок, количество комбинаций в каждом из которых считается достаточно просто. Примеры применения этого правила мы рассмотрим позднее при решении конкретных задач.
Правило произведения применяется в тех случаях, когда выбор некоторого количества (k) объектов можно производить последовательно шаг за шагом. Если при этом на первом шаге имеется n1 вариантов выбора, на втором – n2 вариантов выбора, ..., на k-ом – nk вариантов выбора, то общее количество вариантов выбора, а значит и общее количество таких k-расстановок равно произведению n1 ´ n2 ´... ´ nk.
Пример 3.1. Имеется 5 кусков материала разных цветов. Нужно сшить из них полосатый флаг, состоящий из 3 разноцветных полос. Сколько различных флагов можно сшить?
Решение. Последовательность составления флага можно разбить на 3 шага, на каждом из которых выбирается материал для соответствующей полосы флага. При выборе материала для первой полосы имеется, очевидно, 5 возможностей (n1 = 5). После того как материал для первой полосы выбран, для выбора второй полосы остается только 4 возможности (n2 = 4). После выбора первых двух полос для выбора третьей полосы остается 3 возможности (n3 = 3). По правилу произведения получаем, что общее количество вариантов выбора, то есть
общее количество различных флагов, которые можно сшить из имеющихся материалов, равно 5 ´ 4 ´ 3 = 60.
3.3. Простейшие задачи пересчета
3.3.1. Определение числа k-размещений из n элементов
Число таких размещений принято обозначать 
. При
составлении таких размещений в нашем распоряжении имеется n различных элементов,
из которых нужно выбрать k элементов. При выборе первого элемента у нас
имеется, очевидно, n возможностей, при выборе второго – (n – 1) возможность
(так как из имеющихся n элементов один уже использован на первом шаге), при
выборе третьего элемента – (n – 2) возможности, ..., при выборе k-го элемента –
(n – k + 1) возможность. По правилу произведения получаем:
Умножим и разделим правую часть выражения (3.1) на (n – k)!:
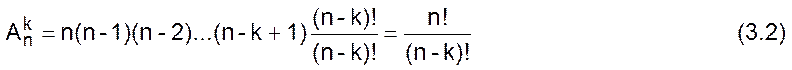
Пример 3.2. Рассмотрим задачу с флагами из примера 3.1. Флаг в этом примере можно рассматривать как размещение из 5 элементов по 3. Общее количество таких размещений по формуле (3.2)
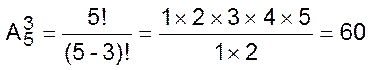
3.3.2. Определение числа k-размещений из элементов n типов с повторениями
Имеются элементы n типов. Количество элементов каждого типа не ограничено. Из
этих элементов нужно выбрать k элементов, причем в расстановке можно использовать
однотипные элементы. Подсчитаем общее количество таких расстановок (его принято
обозначать 
).
При составлении таких расстановок число вариантов выбора на каждом шаге остается одним и тем же и равным n (так как число объектов каждого типа по условию задачи не ограничено и объекты в расстановке могут повторяться, т.е. объект, выбранный на каком-то из предыдущих шагов, можно выбрать снова). Таким образом,
Пример 3.3. Как известно, азбука Морзе состоит из комбинаций элементов двух типов: точек и тире. Причем комбинация может включать от одного до 5 элементов, которые могут повторяться. Определить, сколько различных комбинаций такого типа существует, иначе говоря, сколько различных символов можно передать с помощью азбуки Морзе.
Решение. Комбинацию элементов азбуки Морзе можно рассматривать как размещение из элементов 2 типов по k, где k = 1, 2, 3, 4, 5. Все комбинации символов азбуки Морзе можно разбить на 5 непересекающихся подмножеств по количеству символов в комбинации. Следовательно, можно применить правило суммы:
3.3.3. Определение числа n-перестановок
Перестановка есть частный случай размещения, в котором используются все n имеющихся в нашем распоряжении элементов. Число n-перестановок принято обозначать Pn. Из определения перестановки следует, что число n-перестановок равно числу размещений из n элементов по n:
3.3.4. Определение числа n-перестановок из элементов k типов с повторениями
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.