Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 10

   Если Dх подобен Dy и Dy подобен Dz, то Dх подобен Dz.

1.4.2.5. Виды отношений

Отношение эквивалентности

   Отношение R называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.

   Примеры: подобие треугольников, параллельность прямых и т.п.

Отношение частичного порядка

   Отношение R называется отношением частичного порядка, если оно одновременно рефлексивно, транзитивно и антисимметрично.

   Примеры: отношение делимости на множестве натуральных чисел, отношение нестрогого неравенства на множестве вещественных чисел, отношение включения на множестве подмножеств некоторого множества.

Отношение строгого частичного порядка

   Отношение R называется отношением строгого частичного порядка, если оно транзитивно и асимметрично.

   Пример: строгое неравенство на множестве вещественных чисел.

ТЕМА 2. ТЕОРИЯ ГРАФОВ

2.1. Основные понятия и определения

2.1.1. Определение графа

   Графом называется пара (Х,Г), где Х - некоторое непустое множество, а
Г Í  Х´Х, т.е. граф – это отношение на множестве Х.

   В теории графов Г часто называют отображением Х в себя.

2.1.2. Способы задания

   Графы задаются так же, как и отношения.

а) аналитический способ задания: задаются Х и Г (т.е. множество входящих в Г пар) или Х и множество образов всех элементов множества Х.

Пример 2.1.

   Х = {х₁,...,х₅};  {Гх₁ = {х₂, х₅},  Гх₂ = {х₁, х₃, х₄};  Гх₃ = Æ; Гх₄ = {х₁, х₂, х₅};
Гх₅ = {х₃, х₅}} = Х/Г – фактор-множество множества Х по отображению Г.

б) графический способ задания: множество Х изображается в виде точек на плоскости, называемых вершинами графа; отображение Г задается линиями со стрелками, направленными от вершин к их образам. Эти линии называются
дугами. Если две вершины соединены дугой, то они называются смежными.

   Дуга, идущая из некоторой вершины в ту же самую вершину, называется
петлей.

Пример 2.2.

   Граф из предыдущего примера:

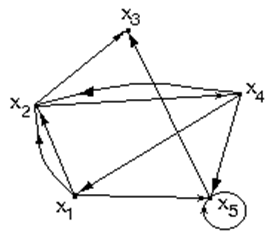
в) матричный способ

   При матричном способе задания каждой вершине графа ставится в соответствие строка и столбец матрицы. Если из вершины x_i в вершину x_j идет дуга, т.е. вершина x_j входит в состав образа вершины x_i (x_j Î Гx_i), то на пересечении строки x_i и столбца x_i ставится 1, в противном случае - 0. Такая матрица называется матрицей смежности графа.

Пример 2.3.

   Граф из предыдущего примера имеет следующую матрицу смежности:

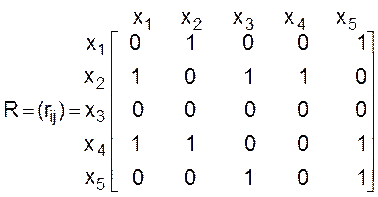
    Если для какой-либо пары вершин (x_i, x_j) r_ij = r_ji, то в графическом представлении часто вместо пары противоположно направленных дуг изображают линию без стрелки, которую называют звеном.

   Граф, состоящий только из звеньев, называется неориентированным графом, или сокращенно неографом.

   Граф, в котором звенья отсутствуют, называется ориентированным графом, или орграфом.

   Если в графе есть и дуги, и звенья, то он называется смешанным.

   Совокупность дуг и звеньев принято называть ребрами.

Пример 2.4.

   а) план города можно представить в виде графа, вершинам которого соответствуют перекрестки, а ребрам – улицы, причем улицам с односторонним движением ставятся в соответствие дуги, а улицам с двусторонним движением – звенья.

   б) результаты шахматного турнира можно представить в виде графа, в котором вершинам соответствуют игроки, дуга идет от победителя к побежденному, а звено связывает участников, сыгравших вничью.

   Иногда наряду с орграфом или смешанным графом необходимо рассматривать неограф, отличающийся от исходного графа только тем, что все дуги заменены звеньями. Такой неограф называется соотнесенным.

   Если вершина является началом или концом какого-либо ребра, то говорят, что эта вершина инцидентна этому ребру (дуге, звену), а ребро инцидентно этой вершине.

   Вершина, не инцидентная ни одному ребру графа, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом.

   Граф называется полным, если в нем любая пара вершин соединена между собой хотя бы в одном направлении.