В отличие от обычных отношений пары вершин могут быть соединены несколькими ребрами, имеющими одну и ту же ориентацию. Такие ребра называются кратными, а граф, в котором имеются кратные ребра, называется мультиграфом. Количество ребер, связывающих в мультиграфе две смежные вершины, называется кратностью. Кратность ребра (xi, xj) обозначается r(xi, xj). Эта величина ставится в матрице смежности вместо единиц и нулей.
Пример 2.5.
а) план города, где имеются улицы с многополосным движением: каждая дуга означает полосу движения; кратность - количество полос для движения в одном направлении;
б) результаты турнира, проводящегося в несколько кругов: кратность – количество побед одного участника над другим.
Иногда возникает необходимость указания на графе дополнительной информации об объектах, представленных ребрами графа, например, длины участка дороги или ее пропускной способности, или мощности линии электропередачи и т.п. Эта информация записывается при графическом представлении графа рядом с дугой, а при матричном представлении – вместо единицы, указывающей на наличие связи между вершинами. Эта величина называется мерой ребра, а соответствующая матрица называется матрицей мер. Меру ребра (xi, xj) будем
обозначать m (xi, xj). Соответствующий граф будем называть графом с нагруженными ребрами.
2.1.3. Пути, контуры, цепи и циклы в графе
Путем в графе называется любая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей дуги.
Путь называется простым, если он не содержит повторяющихся дуг. В противном случае путь называется составным.
Простой путь называется элементарным, если он не содержит повторяющихся вершин.
Контуром в графе называется конечный путь, у которого начальная и конечная вершина совпадают. Как и другие пути, контуры могут быть простыми, составными и элементарными, причем контур называется элементарным, если в нем ни одна вершина не встречается дважды, кроме начальной и конечной (которые совпадают).
В неографах аналогом пути является цепь (составная, простая, элементарная), а аналогом контура – цикл (составной, простой, элементарный).
Количество ребер, из которых состоит путь (цепь, контур, цикл), называется его длиной. При определении длины составного пути (цепи, контура, цикла) повторяющиеся ребра учитываются столько раз, сколько они встречаются в этом пути.
Пример 2.6.
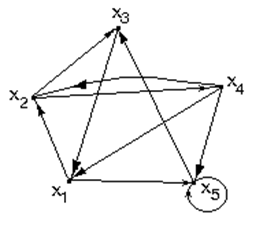
В этом графе путь (х1, x2, x4, x1, x2, x3) является составным, так как в нем дуга (х1, x2) встречается дважды; путь (x2, x4, х1, x2, x3) - простой, но не элементарный, так как в нем вершина x2 встречается дважды; путь (x4, х1, x2, x3) - элементарный, так как он не содержит повторяющихся вершин.
В этом графе контур (x4, x2, x4, х1, x2, x4) - составной, (х1, x5, x3, х1, x2, x4, х1) – простой, но не элементарный, (х1, x2, x4, х1) – элементарный.
2.2. Операции над графами
Над графами выполняются те же операции, что и над отношениями на множествах. Особенности имеют место только в композиции мультиграфов.
Пусть G1 = (Х, Г1) и G2 = (Х, Г2) -
два графа, заданных на одном и том же множестве вершин Х. Рассмотрим их
композицию, которая представляет собой граф на том же множестве вершин. Если
это обычные графы, то в их композиции
G1 ° G2 дуга (xi,
xj) существует тогда и только тогда, когда существует путь (xi,
xk, xj), состоящий из двух ребер, в котором дуга (xi,
xk) принадлежит графу G1, а дуга (xk, xj)
принадлежит графу G2. Если таких путей несколько, то в композицию
все равно включается только одно ребро.
Если же G1 и G2 – мультиграфы, то в их композицию
включается столько дуг
(xi, xj), сколько существует путей длины 2 вида (xi,
xk, xj), в которых дуга (xi, xk)
принадлежит графу G1, а дуга (xk, xj) – графу
G2.
Пример 2.7.
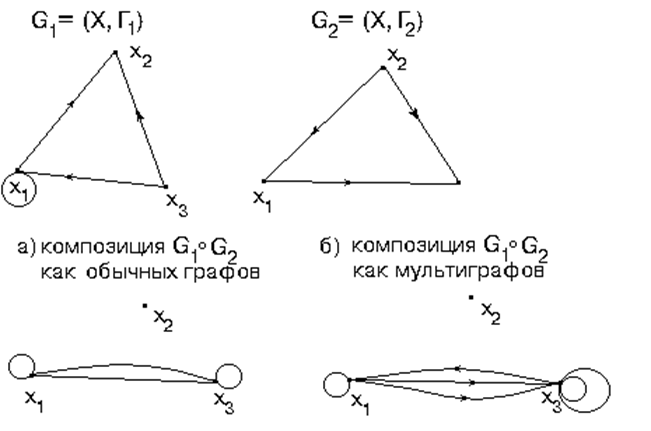
На следующем рисунке представлены два графа G1 = (Х, Г1) и
G2 = (Х, Г2) и их композиции: а) для случая, когда оба эти графа рассматриваются как обычные графы; б) для случая, когда эти графы рассматриваются как мультиграфы с однократными ребрами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.