Конечный индекс этой дуги lj заменяется индексом lj', равным сумме начального индекса и меры ребра:
lj' = li + m (хi, хj).
Очевидно, что lj'< lj, т.е. в результате выполнения этой операции значение индекса конечной вершины убывает.
Эта процедура повторяется до тех пор, пока в графе имеются ребра, удовлетворяющие условию (2.2).
Можно доказать, что через конечное число шагов процесс уменьшения индексов заканчивается в связи с отсутствием ребер, удовлетворяющих условию (2.2). При этом установившиеся значения индексов li равны длинам кратчайших путей от вершины х0 до вершины хi, в частности ln определяет длину кратчайшего пути от х0 до хn.
3-й этап. Строится кратчайший путь между вершинами х0 и хn. Построение ведется в обратном направлении, т.е. от вершины хn к вершине х0. Для этого сначала ищется вершина (обозначим ее хр1), которая была последней использована для уменьшения индекса вершины хn. Из описания предыдущего этапа следует, что разность индексов этих вершин равна мере связывающего их ребра. Далее аналогично ищется вершина хр2, которая последней была использована для уменьшения индекса вершины хр1, и т.д. Через конечное число шагов приходим в начальную вершину х0. Вершины, найденные в результате этой процедуры, взятые в противоположном порядке, и образуют искомый кратчайший путь из х0 в хn.
Этот алгоритм пригоден как для ориентированных, так и для неориентированных графов. Его можно использовать также для графов с ненагруженными ребрами, полагая меры всех ребер равными 1, хотя для таких графов существуют и другие алгоритмы поиска кратчайшего пути.
Пример 2.11. Ниже приведен пример поиска кратчайшего пути в графе из вершины х0 в вершину х7. Последовательно получаемые на втором этапе индексы вершин приведены в скобках около каждой вершины. Следует иметь в виду, что эти последовательности зависят от того порядка, в котором рассматриваются ребра графа, удовлетворяющие условию (2.2), но конечный результат будет одним и тем же.
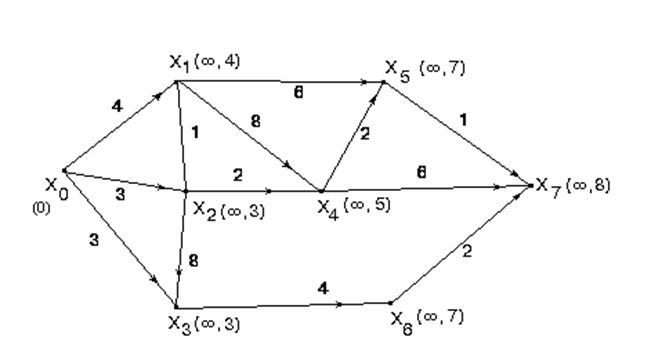
Последней для уменьшения индекса вершины х7 была использована вершина х5 (как нетрудно убедиться, разность индексов этих вершин (8 – 7) как раз равна мере соединяющего их ребра (х5, х7)). Индекс вершины х5 последний раз был уменьшен из вершины х4 (7 – 5 = 2), вершины х4 – из вершины х2, вершины х2 – из вершины х0. Таким образом, кратчайший путь из вершины х0 в вершину х7 проходит через вершины х0, х2, х4, х5, х7 и имеет длину 8.
Поиск длиннейшего пути.
1-й этап. Всем вершинам присваиваются начальные индексы, равные 0.
2-й этап. Ищется дуга (хi, хj), для которой разность между конечным и начальным индексом меньше меры этой дуги:
lj - li < m (хi, хj) (2.3)
Конечный индекс этой дуги lj заменяется индексом lj', равным сумме начального индекса и меры ребра:
lj' = li + m (хi, хj).
Очевидно, что lj' > lj, т.е. в результате выполнения этой операции значение индекса конечной вершины возрастает.
Эта процедура повторяется до тех пор, пока в графе имеются ребра, удовлетворяющие условию (2.3).
Можно доказать, что через конечное число шагов процесс увеличения индексов заканчивается в связи с отсутствием ребер, удовлетворяющих условию (2.3). При этом установившиеся значения индексов li равны длинам длиннейших путей от вершины х0 до вершины хi, в частности ln определяет длину длиннейшего пути от х0 до хn.
3-й этап. Строится длиннейший путь между вершинами х0 и хn. Построение ведется в обратном направлении, т.е. от вершины хn к вершине х0. Для этого сначала ищется вершина (обозначим ее хр1), которая была последней использована для увеличения индекса вершины хn. Из описания предыдущего этапа следует, что разность индексов этих вершин равна мере связывающего их ребра. Далее аналогично ищется вершина хр2, которая последней была использована для увеличения индекса вершины хр1, и т.д. Через конечное число шагов приходим в начальную вершину х0. Вершины, найденные в результате этой процедуры, взятые в противоположном порядке, и образуют искомый длиннейший путь из х0 в хn.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.