Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 2

     4) А I = I;

     5) A Æ = A.

1.2.2. Пересечение

Определение. Пересечением двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые входят во множества А и В одновременно.

Обозначение:

Если С = А  В, то С = {c| cÎА и сÎВ}

Представление пересечения на диаграмме Эйлера-Венна (результат пересечения закрашен):

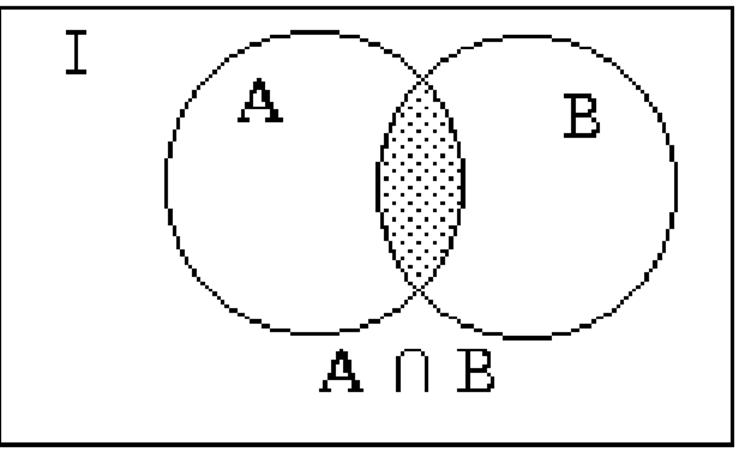
Примеры:

1) А = {a, b, c, d}, B = {c, d, e, f}, C=A B={c, d}

2) Z⁺ – множество целых положительных чисел;

  Z^- – множество целых отрицательных чисел;

  О = {0};

  C = Z⁺ Z^-  O = Æ – так как не существует чисел, одновременно положительных, отрицательных и равных нулю.

3) А – множество студентов гр. ВИ-51, учащихся на отлично;

  В – множество студентов гр. ВИ-51, учащихся без троек;

  С – множество студентов гр. ВИ-51, имеющих удовлетворительные оценки;

  D - множество студентов гр. ВИ-51, имеющих неудовлетворительные оценки;

  E = A B C D = Æ, так как нет ни одного студента, который бы одновременно входил во все четыре множества A,B,C и D.

  F = A B = A, так как каждый студент, учащийся на отлично, не имеет троек, но студент, не имеющий троек, не обязательно учится на отлично.

Свойства: 1) коммутативность (переместительный закон)

               А В = В А

     2) ассоциативность (сочетательный закон)

           А В С = (А В) С = А (В С)

     3) если АÌВ, то А В=А;

     4) А I = А;

     5) A Æ = Æ.

     6) дистрибутивность (распределительный закон) пересечения относительно объединения

        А (В С) = (А В) (А С)

     7) дистрибутивность (распределительный закон) объединения относительно пересечения

        А (В С) = (А В) (А С)

1.2.3. Разность и дополнение

Определение Разностью между множеством А и множеством В называется множество, состоящее из всех тех и только тех элементов, которые входят во множество А и не входят во множество В.

Обозначение: \

Если С = А\В, то С = {c| cÎА и сÏВ}

Представление разности на диаграмме Эйлера-Венна (разность закрашена):

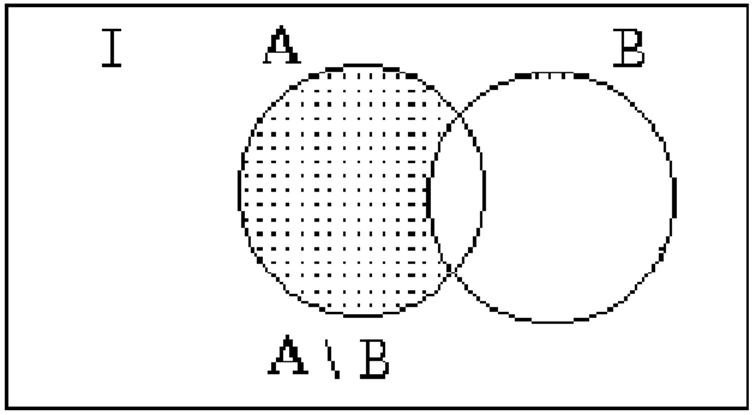
Примеры:

1) А = {a, b, c, d}, B = {c, d, e, f}, C=A\B={a, b}

2) Z⁺ – множество целых положительных чисел;

  Z^- – множество целых отрицательных чисел;

  C = Z⁺\Z^- = Z⁺ - так как у множеств Z⁺ и Z^- нет общих элементов одновременно положительных, отрицательных и равных нулю.

3) А - множество студентов гр. ВИ-51, учащихся на отлично;

  В - множество студентов гр. ВИ-51, учащихся без троек;

  С - множество студентов гр. ВИ-51, имеющих удовлетворительные оценки;

  D = A\B = Æ, так как все отличники не имеют троек, т.е. АÌВ.

  E = В\А - множество студентов, учащихся на хорошо и отлично.

  F = C\A = C, так как ни один элемент А не входит в С.

Определение: Дополнением множества А называется разность I\A.

Обозначение:

Представление дополнения на диаграмме Эйлера-Венна (дополнение закрашено):

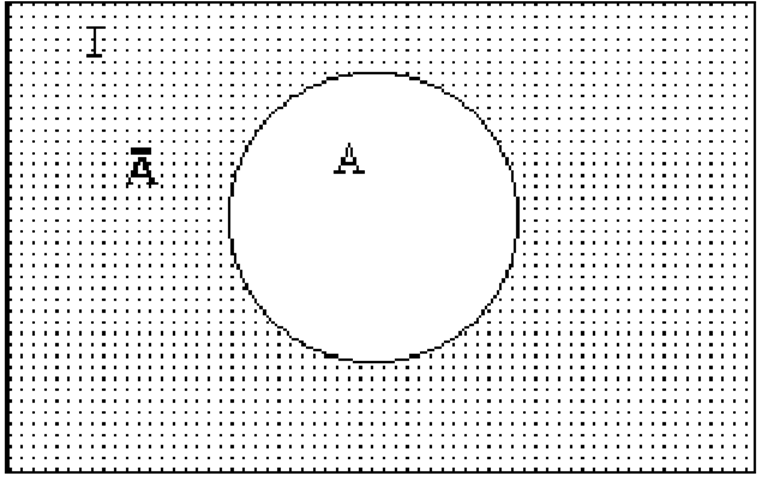
Примеры: 1) I = R - множество вещественных чисел;

С - множество рациональных чисел;

                      - множество иррациональных чисел;

                     2) I = Z - множество целых чисел;

                      N – множество натуральных чисел;

– множество целых неположительных чисел.

                     3) I – множество студентов группы ВИ-51;

                         А – множество успевающих студентов группы ВИ-51;

                      – множество неуспевающих студентов группы ВИ-51.

1.2.4. Декартово произведение множеств

Определение. Декартовым произведением двух множеств (А и В) называется множество всех возможных упорядоченных пар, в каждой из которых первый элемент принадлежит первому множеству (А), а второй элемент принадлежит второму множеству (В).

Обозначение: ´

Если С = А´В, то С = {(a, b)| aÎА, bÎВ}

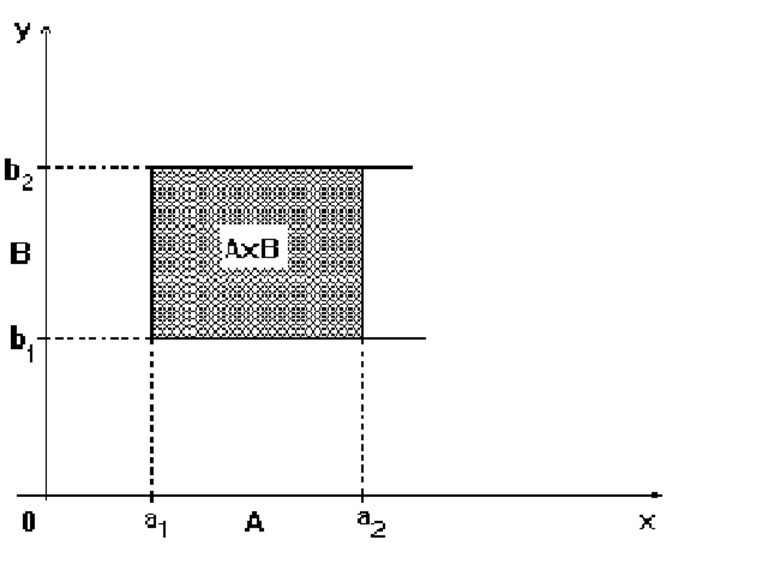
Геометрическое представление декартова произведения.

Пусть А и В - произвольные подмножества множества вещественных чисел:
А = [а₁,а₂], В = [b₁,b₂]. Отложим отрезок А на оси абсцисс, отрезок В на оси ординат. Тогда пара чисел (a, b), где aÎА, а bÎВ определяет точку на плоскости, а декартово произведение А´В образует множество точек прямоугольника со сторонами А и В: