Так как занятия ведутся в каждой учебной группе, то область значений этого отображения совпадает с областью прибытии и Г есть отображение множества преподавателей Х на множество учебных групп Y.
Пример 1.10.
Пусть X = Y = R - множество вещественных чисел и Г = {(x, y) | y = cos x}. Так как косинус определен для любого вещественного числа, то Г является отображением множества вещественных чисел.
Так как косинус принимает не любые значения, а только значения в диапазоне от -1 до +1, то Г есть отображение множества вещественных чисел в себя.
Частным видом отображения является функция. Отображение называется функцией, если каждый элемент области определения отображается ровно в один элемент области значений.
Пример 1.11.
Отображение из примера 1.10 является функцией, так как для каждого значения х существует только одно значение косинуса, а отображение из примера 1.9 функцией не является, так как преподаватель может вести занятия в нескольких группах.
Пример 1.12.
Пусть X = Y = R - множество вещественных чисел, Г = {(x, y)| y = tg x}. Это соответствие не является отображением, так как тангенс определен не для любых вещественных чисел (например, tg (p/2) = ¥), следовательно, с точки зрения введенных определений он не является и функцией. Однако, это утверждение справедливо только при принятом определении области отправления (Х = R).
Если принять, что Х = ] - p/2,+ p/2 [, а Y = R, то тангенс будет функцией, отображающей Х на Y.
Пример 1.13.
Пусть соответствие q = <X,Y,Q> задано матрицей
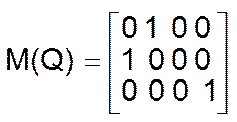
Так как в каждой строке этой матрицы имеются единицы, то это соответствие является отображением (каждому элементу множества Х соответствует хотя бы один элемент множества Y), то Q - отображение, причем отображение Х в Y (почему?). Так единиц в каждой строке имеется ровно по одной, то это отображение является функцией.
Ответьте, является ли функцией обратное соответствие Q-1?
1.4.5. Отношения
1.4.5.1. Определение
Отношением называется соответствие, в котором область отправления совпадает с областью прибытия.
Пусть <X,Y,R> - соответствие, в котором X = Y, то есть отношение. Так как области отправления и прибытия совпадают, то в описании отношения указывается только одно из этих множеств. Таким образом, отношение представляет собой пару <X,R>, где R Í Х´Х.
Такое отношение называют бинарным отношением на множестве Х.
Оно состоит из множества пар (хi, хj), в которых хiÎХ и хjÎХ.
Понятие отношения можно распространить и на случай декартова произведения большего
числа множеств Х ´ Х ´...´
Х, т.е. считать, что в паре <X,R>
R Í Х´Х´...´Х.
Если декартово произведение содержит n сомножителей, то отношение называют
n-арным. Оно состоит из упорядоченных наборов по n элементов, каждый из которых
принадлежит множеству Х:
___
R = {(x1, x2, ... ,xn) | хiÎХ, i=1,n}
Пример 1.14. Операция сложения на множестве вещественных чисел a+b=c может рассматриваться как тернарное отношение на этом множестве (тернарное означает, что декартово произведение содержит три сомножителя):
R = {(a, b, c)| a, b, c Î E, (a, b, c) Í Е´Е´Е},
где Е - множество вещественных чисел.
Пропорция
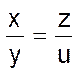
может рассматриваться как 4-арное отношение на множестве вещественных чисел
R = {(x, y, z, u) | x, y, z, u Î E, (x, y, z, u) Í Е´Е´Е´Е}.
Далее мы будем рассматривать только бинарные отношения. При этом тот факт, что (x, y) Î R, будем обычно записывать xRy (читается: х находится в отношении R к y).
Пример 1.15.
Пусть Х - множество людей. Будем считать, что xRy означает, что "х – брат y". Тогда
R = {(x, y) | х, y Î Х, х – брат y}
есть отношение на множестве людей.
Пример 1.16.
Пусть Х - множество вещественных чисел.
R = {(x, y) | х, y Î Х, х = tg y} – отношение на множестве вещественных чисел.
Пример 1.17.
Пусть Х = {1, 2, 3, 4, 5, 6}.
R = {(x, y) | х, y Î Х, х – делитель y}.
1.4.5.2. Задание отношений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.