Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 5

   Если соответствие задано в матричном виде, то для получения обратного соответствия матрицу нужно транспонировать, т.е. поменять местами ее строки и столбцы.

   Если соответствие задано графически, то для получения обратного соответствия нужно изменить направление всех стрелок на противоположное.

Пример 1.4.

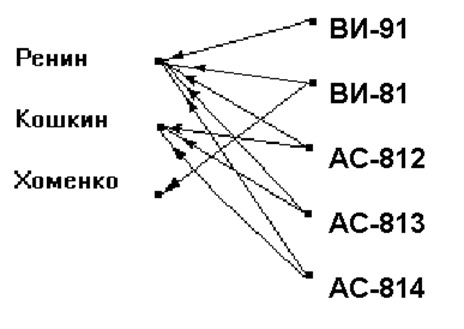
   Выполним симметризацию соответствия из предыдущего примера.

   Q={(ВИ-91, Ренин), (АC-812, Ренин), (АC-813, Ренин), (АC-814, Ренин),
(АC-812,Кошкин), (АC-813, Кошкин), (АC-814, Кошкин), (ВИ-31, Хоменко)}

   В матричной форме:

		Ренин	Кошкин	Хоменко
M(Q-1) =	ВИ-91	1	0	0
	ВИ-81	1	0	1
	АС-812	1	1	0
	АС-813	1	1	0
	АС-814	1	1	0

   В графической форме:

1.4.3.4. Композиция соответствий

   Пусть даны два соответствия

                           q = <X,Y,Q>, Q Í X´Y и p = <Y,Z,P>, P Í Y´Z.

   Композицией соответствий q и p называется соответствие s = q_°p = (X,Z,S),
S = Q_°PÍ X´Z, состоящее из таких и только таких пар (x, z), xÎX, zÎZ, для которых существует хотя бы один элемент yÎY, такой, что пара (x, y)ÎQ, а пара
(y, z) ÎP.

   Из этого определения следует, что областью отправления композиции является область отправления первого из соответствий, образующих композицию, а областью прибытия – область прибытия второго соответствия. Для того чтобы пара (x, z), xÎX, zÎZ, принадлежала композиции, должен существовать промежуточный элемент во множестве Y, образующий с элементами x и z пары, входящие в исходные соответствия. Это можно кратко записать таким образом:

   Если S = Q_°P, то (x, z) ÎS <=> $yÎY ((x, y) ÎQ L (y, z) ÎP                             (1.1)

   В формуле (1.1) использованы следующие обозначения:

   <=> -"тогда и только тогда";

   $ - "существует хотя бы один";

   L - "и".

Пример 1.5.

   Пусть Х - множество кафедр НГТУ; Y - множество учебных дисциплин, входящих в учебные планы университета; Z - множество специальностей, по которым ведется подготовка, и пусть Q = {(x, y)| кафедра х может вести занятия по дисциплине y}; P = {(y, z)| дисциплина y входит в учебный план специальности z}.

   Тогда композиция Q_°P = {(x, z)| кафедра х может вести занятия для специальности z}, иначе говоря, пара (х, z)ÎQ_°P тогда и только тогда, когда существует дисциплина y из множества учебных планов университета, которая входит в учебный план специальности z и которую может вести кафедра х.

Пример 1.6.

   Пусть Х = Y = Z = R - множество вещественных чисел и пусть
Q = {(x, y)| y = sin x}, P = {(y, z)| z = ln y}. Тогда S = Q_°P = = {(x, z)| z = ln (sin x)}.

   Проанализируем области определения и значений исходных соответствий Q и P и их композиции.

   Так как функция sin x определена на всей числовой оси, то областью определения первого соответствия Q является все множество Х (Пр₁Q = R). Так как синус принимает значения только в диапазоне от -1 до +1, то областью значений первого соответствия будет замкнутый отрезок [-1;1] (Пр₂Q = [-1;1]).

   Так как логарифмы определены только для положительных чисел, то

 В области определения логарифмы могут принимать любые вещественные значения (), следовательно, Пр₂Р = R.

   Функция ln (sin x) определена для тех значений х, при которых sin x > 0, т.е. Пр₁S = {x| sin x > 0}. При этом логарифм может принимать значения от -¥(при x®0) до 0 (при sin x = 1). Таким образом, Пр₂S = ]-¥,0].

   Из этого примера видно, что область определения композиции может не совпадать с областью определения первого соответствия, а область значений композиции может не совпадать с областью значений второго соответствия.

   Если множества X, Y и Z, для которых определены соответствия, конечны, то операцию композиции можно выполнить графическим или матричным способом.