Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 3

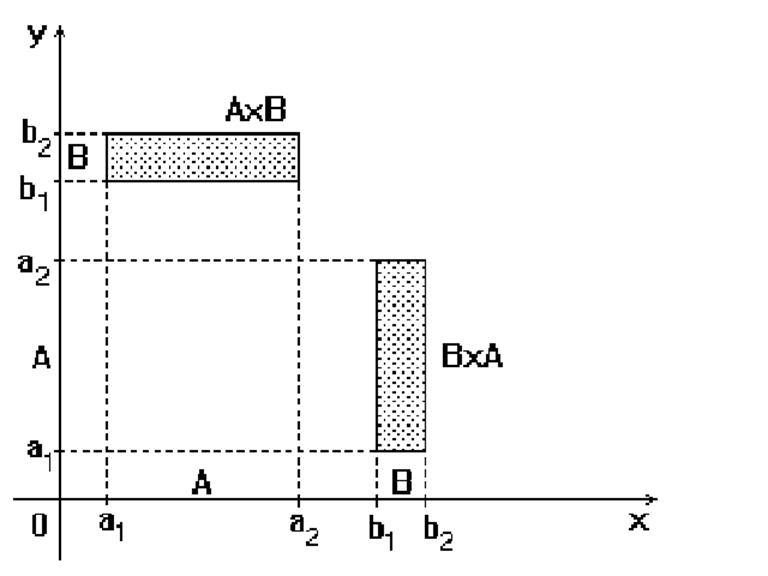
В отличие от объединения и пересечения декартово произведение некоммутативно, то есть А´B ¹ B´A, что хорошо видно на графическом представлении декартова произведения:

1.3. Алгебра множеств

Определение. Совокупность всех множеств, входящих в универсальное множество I, совместно с операциями объединения ( ), пересечения

( ) и дополнения называется булевой алгеброй множеств.

   Как и всякая алгебра, булева алгебра множеств имеет дело с некоторыми объектами, объединяемыми по определенным правилам в формулы с помощью знаков операций и скобок.

   В обычной алгебре эти объекты – числа или заменяющие их символы, в алгебре множеств – это множества или заменяющие их символы.

   Формулы алгебры множеств строятся по следующим правилам:

   1) всякий символ, обозначающий множество, есть формула алгебры множеств;

   2) если Y и Θ – формулы алгебры множеств, то

     (), (Y) (Θ), (Y) (Θ) - тоже формулы алгебры множеств.

                                                           _________

Примеры: А, В, (А) (В), (А) (В), ((А) (В)) ((А) (В))

Для упрощения записи скобки вокруг отдельных символов, обозначающих множества, опускают. Опускают также внешние скобки под знаком дополнения. Кроме того, как и в обычной алгебре, вводят правило старшинства операций. В частности, принято, что при отсутствии скобок первыми выполняются дополнения, относящиеся к отдельным множествам, затем пересечения, после них объединения. В последнюю очередь выполняются дополнения, относящиеся к комбинациям множеств. Скобки используют только для изменения порядка выполнения операций.

Пример: последняя формула из предыдущего примера может быть записана так:              
                                                  ______

                                                  А В А В

   Если в формулу алгебры множеств подставить вместо символов конкретные множества и выполнить указанные в формуле операции, то получится конкретное множество.

   Обычно одно и то же множество можно представить несколькими различными формулами, например, А В = В А.

   Различные формулы, представляющие одно и то же множество, называются эквивалентными. Алгебра множеств занимается правилами эквивалентного или тождественного преобразования формул.

   Все тождественные преобразования формул алгебры множеств основаны на следующих основных тождественных соотношениях:

1)А В = В А - коммутативность объединения;

2)А В = В А - коммутативность пересечения;

3)А (В С) = (А В) С - ассоциативность объединения;

4)А (В С) = (А В) С - ассоциативность пересечения;

5)А А = А - идемпотентность объединения;

6)А А = А - идемпотентность пересечения;

7)(А В) С = (А С) ( В С) - дистрибутивность пересечения относительно объединения (1-й дистрибутивный закон);

8)(А В) С = (А С)  (В С) - дистрибутивность объединения относительно пересечения (2-й дистрибутивный закон);

    ______    _       _

9) А В = А В - 1-е правило де Моргана;

      ______    _       _

10) А В = А В - 2-е правило де Моргана;

11) = А - закон двойного дополнения;

12) А (А В) = А - 1-й закон поглощения;

13)А (А В) = А - 2-й закон поглощения;

               _

14) А А = I;

               _

15) А А = Æ;

16) А Æ = А;

17) А Æ = Æ;

18) A I = I;

19) A I = A;

      _

20) I = Æ;

       _

21) Æ = I;

1.4. Соответствия

1.4.1. Определения

Соответствием называется тройка множеств q = <X,Y,Q>, где Х и Y – произвольные множества, а Q Í X´Y.

Таким образом, соответствие состоит из множества упорядоченных пар (x, y), в которых первый элемент xÎХ, а второй элемент yÎY.

При этом Х называется областью отправления соответствия, Y – областью прибытия соответствия, а Q – графиком соответствия (иногда его называют просто соответствием).

Множество первых элементов пар (x, y), принадлежащих Q, называется областью определения или первой проекцией соответствия и обозначается Пр₁Q. Очевидно, что Пр₁Q Í X.

Множество вторых элементов пар (x, y), принадлежащих Q, называется областью значений или второй проекцией соответствия и обозначается Пр₂Q. Очевидно, что Пр₂Q Í Y.

Пример 1.1.