Внимание! Длиннейший путь можно искать только в ориентированных графах, не имеющих контуров!
Пример 2.12. Ниже приведен пример поиска длиннейшего пути в графе. Последовательно получаемые на втором этапе индексы вершин приведены в скобках около каждой вершины.
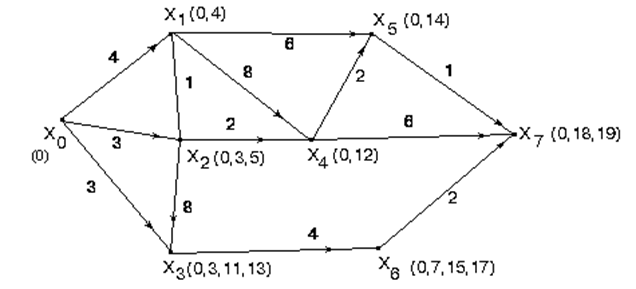
Последней для увеличения индекса вершины х7 была использована вершина х6 (разность индексов 19 – 17 равна мере 2), для х6 -вершина х3 (17 – 13 = 4), для х3 - х2 (13 – 5 = 8), для х2 - х1 (5 – 4 = 1), для х1 - х0 (4 – 0 = 4). Таким образом, длиннейший путь из х0 в х7 имеет вид: х0, х1, х2, х3, х6, х7, и его длина равна 19.
3.1. Основные понятия и определения
Комбинаторика – это раздел математики, изучающий вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, а также, как перечислить все возможные комбинации заданного вида.
В соответствии с этим определением различают два вида комбинаторных задач: пересчет и перечисление. Мы здесь будем рассматривать только задачи пересчета.
Простейшие примеры комбинаций: распределение нового набора студентов, поступивших в университет, по учебным группам; набор гирь, с помощью которого можно взвесить некоторый товар; состав профсоюзного комитета профсоюзной организации; набор ребер, с помощью которого можно построить дерево на заданном множестве вершин, и т.д.
Комбинации объектов в комбинаторике принято называть расстановками. Расстановка – это просто некоторое множество объектов. Отличие от обычного множества состоит в том, что при определенных обстоятельствах, оговариваемых или подразумеваемых в условии задачи, некоторые объекты, входящие в расстановку, могут быть неразличимы между собой с точки зрения рассматриваемой задачи, т.е. в расстановке объекты могут повторяться, тогда как в обычных множествах все элементы считаются различными. Пример расстановки с повторениями: набор гирь, с помощью которого взвешивается товар,
может содержать несколько гирь одинаковой массы, которые с точки зрения решаемой задачи (взвешивание товара) друг от друга неразличимы.
Расстановка, состоящая из k объектов, называется k-расстановкой.
Расстановка, для которой имеет значение порядок следования объектов, называется размещением.
Например, полосатый флаг можно рассматривать как расстановку из некоторого множества полос цветных материалов, а так как порядок следования этих полос имеет значение, то эта расстановка является размещением.
Если для составления размещения нужно выбрать k объектов из некоторого множества,
содержащего n объектов, то такое размещение называется
k-размещением из n элементов или размещением из n элементов по k.
Если в размещение включаются все n имеющихся в нашем распоряжении элементов, то такое размещение называется перестановкой из n элементов или n-перестановкой.
Например, профсоюзная конференция выбрала профсоюзный комитет, который затем распределяет должности между членами комитета. Так как в распределении участвуют все члены комитета, и имеет значение, кому какая должность назначена (т.е. имеет значение порядок распределения членов комитета по должностям), то профсоюзный комитет с точки зрения комбинаторики можно рассматривать как перестановку.
Расстановка, для которой не имеет значения порядок следования элементов, называется сочетанием.
Например, для состава учебной группы не имеет значения, в каком порядке перечислены студенты в журнале, поэтому учебная группа с точки зрения комбинаторики представляет собой сочетание.
Если для составления сочетания нужно выбрать k объектов из некоторого множества,
содержащего n объектов, то такое сочетание называется
k-сочетанием из n элементов или сочетанием из n элементов по k.
3.2. Общие правила комбинаторики
Эти правила используются для подсчета числа расстановок различного типа. Таких правил два: правило суммы и правило произведения.
Правило суммы представляет собой формулировку того очевидного факта, что если некоторое множество (в данном случае множество всех рассматриваемых расстановок) можно разбить на непересекающиеся подмножества, то общее количество элементов множества равно сумме количеств элементов, входящих в отдельные подмножества.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.