Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 6

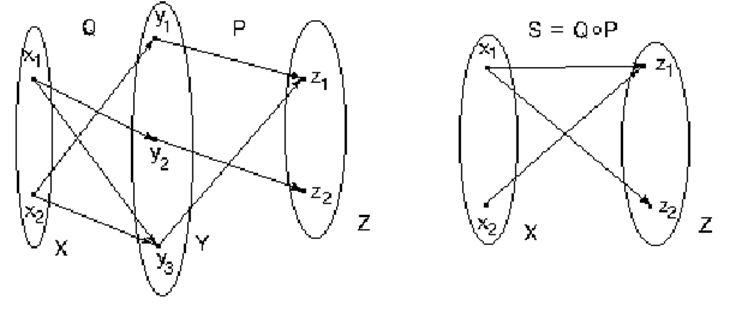
   Для графического выполнения композиции оба  соответствия изображают на одном чертеже, совместив область прибытия первого соответствия с областью отправления второго соответствия. На графическом изображении композиции стрелками соединяют те и только те точки хÎ и zÎZ, которые на совмещенном чертеже исходных соответствий соединены хотя бы одним путем, идущим из х в z.

Пример 1.7.

   Для нахождения композиции соответствий с помощью матриц введем понятие максиминного произведения матриц. Максиминное произведение матриц находится аналогично обычному произведению матриц, но вместо умножения элементов матриц используется операция выбора минимального из двух элементов, а вместо суммирования произведений соответствующих элементов выполняется операция выбора максимального из минимальных элементов. Для вычисления элемента s_ik, стоящего на пересечении i-ой строки и k-го столбца результирующей матрицы, нужно взять i-ую строку первой матрицы и умножить ее максиминно на k-ый столбец второй матрицы, используя формулу

                                               s_ik = max min (q_ij, p_jk),                                               (1.2)

                                                          j

где q_ij – элемент, стоящий на пересечении i-ой строки и j-го столбца первой матрицы, а p_jk – элемент, стоящий на пересечении j-ой строки и k-го столбца второй матрицы.

   Если матрицы состоят, как в нашем случае, только из нулей и единиц, то максиминное произведение называют булевым (по имени известного английского математика, одного из основателей математической логики Джорджа Буля). В этом случае формула (1.2) упрощается, так как если сомножители могут быть только нулями и единицами, то, как легко убедиться, минимальный из них равен их произведению, и формула (1.2) получает вид

                                                    s_ik = max q_ijp_jk,                                                      (1.3)

                                                               j

   Из формул (1.2) и (1.3) следует, что s_ik=1 тогда и только тогда, когда в i-ой строке первой матрицы имеется хотя бы одна единица, стоящая в этой строке на том же месте (j), что и единица в столбце второй матрицы. Сопоставление этого результата с определением композиции соответствий показывает, что если перемножаемые матрицы описывают некоторые соответствия, то их булево произведение описывает композицию этих соответствий.

Пример 1.8.

   Рассмотрим те же соответствия, которые использовались в предыдущем примере для нахождения композиции графическим способом.

.

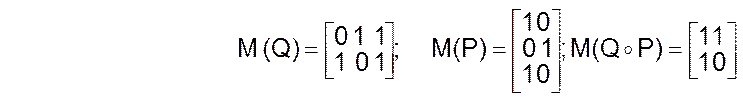Элемент s₁₁, стоящий на пересечении первой строки и первого столбца матрицы M(Q_°P), получается перемножением соответствующих элементов первой строки матрицы М(Q) и первого столбца матрицы М(Р), после чего из полученных произведений выбирается максимальное: s₁₁ = max (0 × 1, 1 × 0, 1 × 1) = 1. Остальные элементы вычисляются аналогично.

   Сопоставление матрицы M(Q_°P) с графическим изображением композиции Q_°P на чертеже из предыдущего примера показывает, что, как и следовало ожидать, результат получается одинаковым.

1.4.4. Отображения

   Пусть задано соответствие <X,Y,Г>, где ГÍX´Y.

   Это соответствие называется отображением множества Х, если область определения этого соответствия совпадает с областью отправления, т.е. Пр₁Г = Х. Если при этом область значений соответствия совпадает с областью его прибытия (Пр₂Г = Y), то говорят, что имеет место отображение множества Х на Y, если же область значений не совпадает с Y (Пр₂ГÌY), то имеет место отображение Х в Y.

   Множество вторых элементов пар, входящих в отображение Г, в которых первым элементом является х, называется образом элемента х и обозначается Гх. Очевидно, что ГхÍX. Если элемент yÎГх, то х называется прообразом элемента y.

Пример 1.9.

   Пусть Х - множество преподавателей НГТУ, Y - множество учебных групп и пусть Г = {(x, y)| преподаватель х ведет занятия в группе y}. Так как все преподаватели ведут учебные занятия, то область определения этого соответствия совпадает с областью отправления Х, следовательно, соответствие Г является отображением.