Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 9

   Рассмотренные свойства преобразований Фурье и вычисленные спектральные функции ряда сигналов являются основой спектральной теории аналоговых детерминированных сигналов. Дальнейшей  задачей нашей работы является изучение экспериментальных методов спектрального анализа различных классов сигналов, в том числе и случайных.

   В современном эксперименте такой анализ выполняется цифровыми методами с применением электронно – вычислительных машин (ЭВМ). При этом исходные аналоговые реализации сигналов переводятся в дискретные. Эту операцию надо производить по определенным правилам, они будут сформулированы в следующем разделе.

Раздел 4. ЗАМЕНА АНАЛОГОВОГО СГНАЛА ЕГО ДИСКРЕТНОЙ РЕАЛИЗАЦИЕЙ

(Теорема Котельникова)

   Преобразование сигналов в дискретную (цифровую) форму выполняется с помощью специальных  электронных приборов – аналого-цифровых преобразователей (АЦП). Однозначность таких преобразований зависит от спектральных свойств  исходных аналоговых сигналов. Рассмотрим этот вопрос подробнее.

     В 1933 году В.А.Котельников доказал теорему, которая является одним  из фундаментальных положений теории цифровых сигналов. Эта теорема устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром по его дискретным выборкам, взятым через равные промежутки времени. В зарубежной литературе эта теорема известна как теорема отсчетов  (sampling theorem).

            Формулировка. Пусть  – непрерывный (аналоговый) сигнал, спектральная плотность которого действительна и ограничена по частоте сверху некоторой граничной частотой .  Пусть имеется также его дискретная по времени реализация взятая через равные промежутки времени   . Тогда исходный сигнал может быть точно восстановлен, если интервал дискретизации равен  .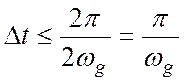

Доказательство. Пусть спектральная плотность сигнала    на бесконечной оси частот имеет вид Рис.1.

                                    Рис.4.1                                                                     Рис.4.2

   В соответствии с условиями теоремы, ограничена по частоте интервалом ω_g, его абсолютная длина, с учетом "отражения" на область отрицательных частот, равна 2ω_g. Тогда  и  связаны обратным преобразованием Фурье:

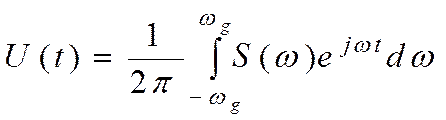                                                                          (4.1)

   Аналитически продолжим функцию с периодом  2 на всю ось ω. Это схематически показано на Рис.4.2. Тогда эту  периодическую функцию можно разложить  по частоте в обобщенный ряд Фурье:

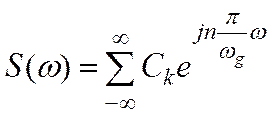                                                            (4.2)

Разложение ведется в уже знакомом нам ортонормированном базисе

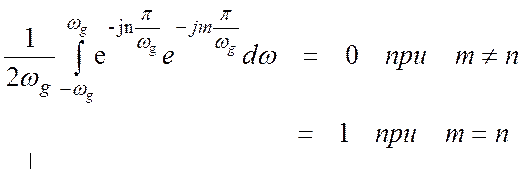                                                                  (4.3)

 Коэффициенты разложения:

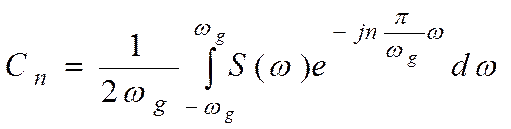                                                              (4.4)                                     

Сравнивая (4.4) и (4.1) видим их очевидное сходство, то есть коэффициенты  можно выразить через исходный сигнал  взятый в дискретные моменты времени с периодом 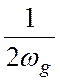. Для этого (4.1) множим на 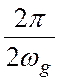и получаем

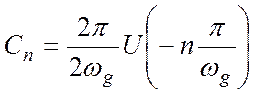                                                                                   (4.5)

Используя выражение для коэффициентов ряда можно записать ряд Фурье (4.2) в виде:

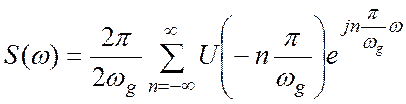                                                                     (4.6)

Заметим, что в выражение (4.6) дискретное время входит со знаком минус. Для того, чтобы вернуться к обычному течению времени, сделаем замену . Результат

суммирования в (4.6) не зависит от знака n , он отразится только в знаке экспоненты. Окончательно разложение для  примет вид:

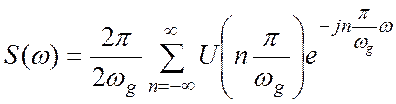                                                                    (4.7)

Подставив (4.7) в (4.1), запишем исходный аналоговый сигнал  в виде:

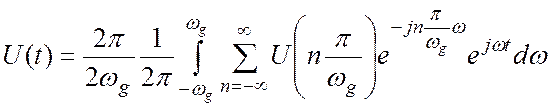                                          (4.8)

Меняем местами порядок суммирования и интегрирования и объединяем показатели экспонент:

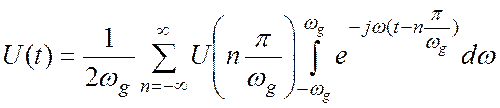                                                                     (4.9)