Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 22

 

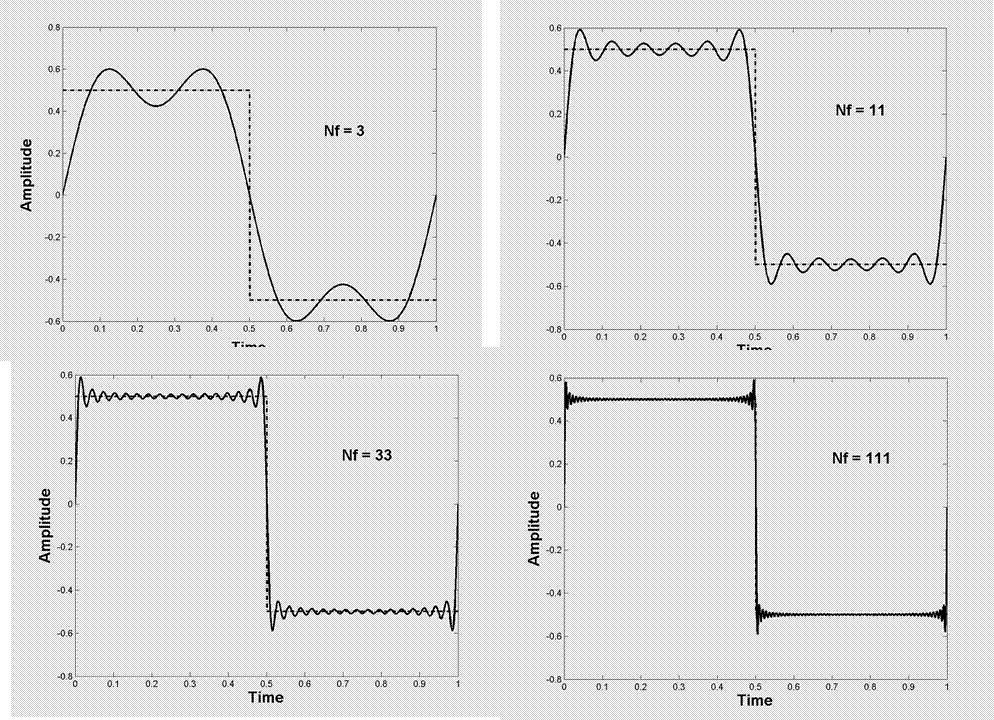
   Видно, как с нарастанием числа удерживаемых гармоник форма сигнала стремится к прямоугольному импульсу.

ПРИЛОЖЕНИЕ 4

Спектральная функция отрезка синусоиды.

  Модельный сигнал такого вида вид показан на Рис.1.1 Приложения 1. Онначинается в некоторый момент времени  и заканчивается в момент , кратный количеству периодов заполнения 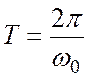. Вне этого временного интервала . Тогда принимая  за начало отсчета времени, спектральная функция  такого сигнала может быть определена следующим образом:

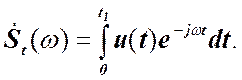
Если ₁ – момент наблюдения, то спектр (1) называется текущим спектром. Такой спектр, вычисленный по формуле (1), уже зависит не только от частоты , но и от времени, в нашем случае от количества периодов сигнала. Исходная модель сигнала:

 

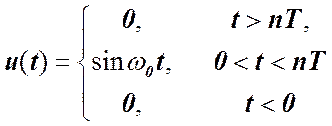
Тогда

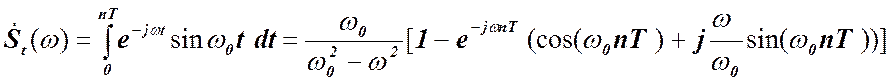Учитывая, что 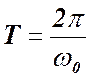, получим

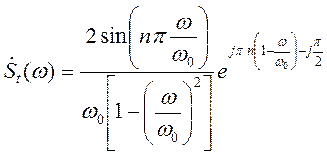
На рис.1. представлены сигналы и модуль их спектров для и . Приведена только область положительных частот.  Видно, что при малом числе периодов спектр сигнала "развален", у него есть боковые максимумы спектральной плотности. Только при стремлении количества периодов к спектр превращается в одиночную линию.

   Ниже приведен листинг соответствующей программы. Читателю предлагается самостоятельно разобраться в ней и построить спектральную функцию отрезков синусоиды для других nT(по собственному выбору).

      В заключение отметим, что рассмотренный вопрос имеет принципиальное значение для практики спектрального анализа сигналов, содержащих несколько гармонических спектральных компонент. Для того, чтобы разрешить их в отдельности, необходимо правильно подбирать длину исследуемой реализации сигнала. Чем выше требуемое разрешение, тем длиннее должна быть реализация.

Попробуйте сгенерировать сигнал из отрезка двух синусоид с близкими частотами и добейтесь их разрешения по частоте. Какой критерий разрешения можно сформулировать?

Листинг программы спектрального анализа отрезка синусоиды

clf; clear; ns=2^4;

N=2^8;

om=1; t=[0:N-1]*2*pi/8;

x1=[ones(1,ns),zeros(1,N-ns)];

x=x1.*sin(om*t);

%fftshift(x);

N1=length(x), k1=[1:N1]; Fmax=1/(2);df=1/(N);

yr=real(fft(x,N)); yi=imag(fft(x,N));

zz=sqrt(yr.^2+yi.^2); y=abs(fftshift(zz));

k=[-Fmax:df:Fmax-df];

length(y), length(k)

figure(1); clf;plot(k,y,'k')

figure(2)

clf;

 axis([0 N,-1.2 1.2]); plot(k1,x,'k'); hold on

ЛИТЕРАТУРА

1.  Спектор С.А.  Электрические измерения физических величин.– Л. Энергоатомиздат,1987г.

2.   Гоноровский И.С., .Демин М.П. Радиотехнические цепи и сигналы. .–М., Радио и связь, 1994.

3.   Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и в других областях.–М., Наука, Гл.ред. физ.-мат.лит., 1989г.

4.   Иванов М.Т, .Сергиенко А.Б, Ушаков В.Н.. Теоретические основы радиотехники.  М., Высшая школа, 2003г.

5.   Поршнев С.В. Компьютерное моделирование физических процессов в пакете МАТЛАБ. –М., Горячая линия – Телеком, 2003.

6.   Сергиенко А.Б. Цифровая обработка сигналов. – СПб., Питер, 2003г.

      7.   Ричард Г.Лайонс. Цифровая обработка сигналов. – М., Бином, 2006г.

      8.   Баскаков С.И. Радиотехнические цепи и сигналы. – М., Высшая школа, 2003г.

      9.   Г.Дженкинс, Д.Ваттс.Спектральный анализ и его приложения. – М., Мир, 1971г.

10.   Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. – М., Мир,  1990г.

11.   Дж. Бендат, А. Пирсол. Измерение и анализ случайных процессов. – М.,Мир, 1974г.

12.   Грибанов Ю.И., Мальков В.Л. Спектральный анализ случайных процессов. – М.,

Энергия, 1974г.

13.   Ж. Макс. Методы и техника обработки сигналов при физических измерениях.– М., Мир, 1983г.

14. Лазарев Ю. Моделирование процессов и систем в МАТЛАБ. – СПб., Питер, 2005г.