 |
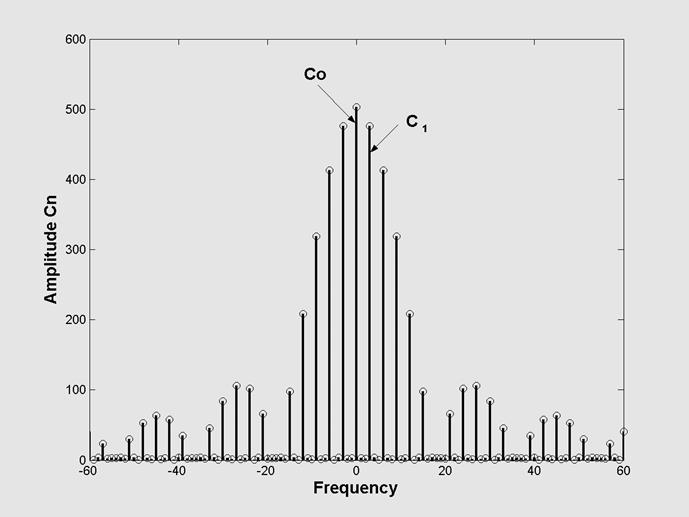
Рис.2.3. Амплитудный спектр последовательности прямоугольных импульсов
На нулевой частоте показана
постоянная составляющая процесса Со . Амплитуда составляющей на основной
частоте 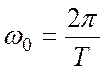 равна С1 такая же
амплитуда у составляющей на отрицательной частоте
равна С1 такая же
амплитуда у составляющей на отрицательной частоте ![]()
![]() . Остальные коэффициенты образуют спектр амплитуд
гармоник на частотах, кратных частотам
. Остальные коэффициенты образуют спектр амплитуд
гармоник на частотах, кратных частотам ![]() . Как уже
отмечалось, физический смысл имеют только спектральные компоненты,
расположенные на положительных частотах. Чтобы получить физический спектр, надо
взять гармоники на положительных частотах и удвоить их амплитуду.
. Как уже
отмечалось, физический смысл имеют только спектральные компоненты,
расположенные на положительных частотах. Чтобы получить физический спектр, надо
взять гармоники на положительных частотах и удвоить их амплитуду.
Очевидно, что функция (2.9) для некоторых номеров гармоник может обращаться в нуль. Для этого случая будет выполняться условие
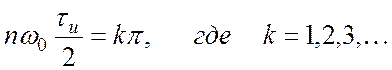 . В частности, для
первого нуля k = 1. Учитывая, что
. В частности, для
первого нуля k = 1. Учитывая, что ![]() находим
этот номер : n1 =
находим
этот номер : n1 = ![]() . В частности, для
осциллограммы Рис.2.2 отношение
. В частности, для
осциллограммы Рис.2.2 отношение ![]() равно шести. Поэтому на
Рис. 2.3 все гармоники, номера которых кратны шести, равны нулю.
равно шести. Поэтому на
Рис. 2.3 все гармоники, номера которых кратны шести, равны нулю.
Можно ввести понятие
"огибающей" спектра Рис.2.3. Очевидно, что она описывается функцией
типа 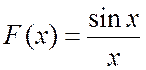 . В общем случае, при уменьшении
. В общем случае, при уменьшении ![]() – длительности импульсов положение нулей
– длительности импульсов положение нулей ![]() смещается в область высоких частот
(спектр становится "шире"). При увеличении
смещается в область высоких частот
(спектр становится "шире"). При увеличении ![]() расстояние
по частоте между гармониками уменьшается, они располагаются ближе друг к другу.
Убедитесь в этом, воспользовавшись материалом Приложения 2, меняя
отношение
расстояние
по частоте между гармониками уменьшается, они располагаются ближе друг к другу.
Убедитесь в этом, воспользовавшись материалом Приложения 2, меняя
отношение ![]() .
.
Рассмотрим теперь вопрос – что
будет, если искусственно оборвать ряд (2.5) и
ограничиться конечным числом членов при разложении ![]() . Если
. Если ![]() содержит разрывы первого рода, то возникает
так называемый эффект Гиббса.. Он заключается в том, что если выполнить
обратное преобразование Фурье усеченного ряда, то вблизи разрывов
содержит разрывы первого рода, то возникает
так называемый эффект Гиббса.. Он заключается в том, что если выполнить
обратное преобразование Фурье усеченного ряда, то вблизи разрывов ![]() возникают колебания. Период колебаний равен
периоду первого отброшенного члена ряда.
возникают колебания. Период колебаний равен
периоду первого отброшенного члена ряда.
 |
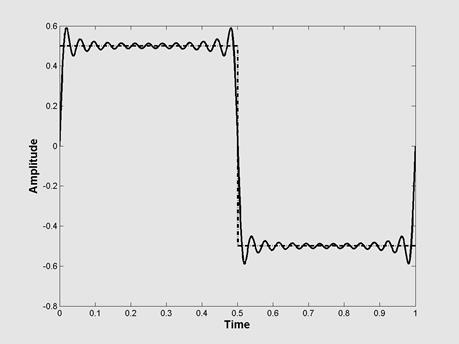 |
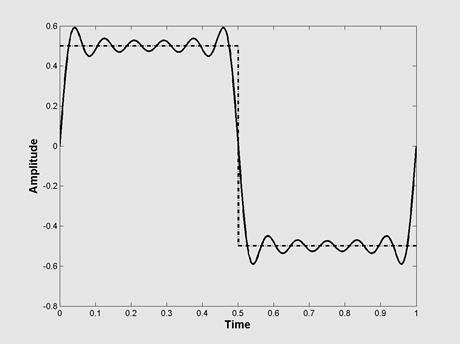
Рис.2.4. Эффект Гиббса при разном числе удерживаемых членов ряда Фурье;
слева – 11 членов, справа – 25 членов.
Покажем, как проявляется эффект Гиббса на примере прямоугольного импульса, у которого длительность равна половине периода повторения. На Рис.2.4 слева показан результат его восстановления по разному числу гармоник. Соответствующая программа демонстрации эффекта Гиббса дана в Приложении 3.
Раздел 3. .СПЕКТРАЛЬНЫЕ ФУНКЦИИ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Непериодические сигналы – это
частный случай периодических сигналов, у которых период повторения равен
бесконечности. Поскольку ![]() то при
то при ![]() расстояние между гармониками становится
бесконечно малым, т.е. спектр становится сплошным. Кроме того, амплитуды
гармоник, вычисленные по ф-ле (2.9) становятся бесконечно малыми.
расстояние между гармониками становится
бесконечно малым, т.е. спектр становится сплошным. Кроме того, амплитуды
гармоник, вычисленные по ф-ле (2.9) становятся бесконечно малыми.
Пользуясь этими соображениями,
получим формулы для спектров непериодических сигналов. Как показано в литературе
по теории сигналов, достаточным, но не необходимым условием существования
преобразования Фурье для непериодических сигналов является абсолютная
интегрируемость ![]() , т.е. должен существовать
интеграл [ 4 ]:
, т.е. должен существовать
интеграл [ 4 ]:
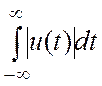 <
< ![]()
Чтобы получить формулы,
описывающие спектр непериодических сигналов, поступим следующим образом.
Непериодический сигнал ![]() длительностью
длительностью ![]() представим в виде его аналитического
продолжения на всю ось
представим в виде его аналитического
продолжения на всю ось ![]() , которое обозначим как периодический
сигнал
, которое обозначим как периодический
сигнал ![]() с периодом
с периодом ![]() .
Разложим
.
Разложим ![]() в ряд Фурье:
в ряд Фурье:
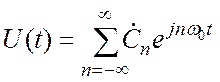 , (3.1)
, (3.1)
где 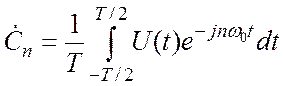 (3.2)
(3.2)
Подставим (3.2) в (3.1) :
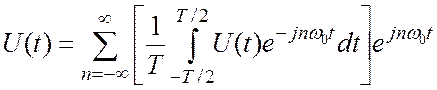
Сделаем замену: ![]() ,
тогда
,
тогда
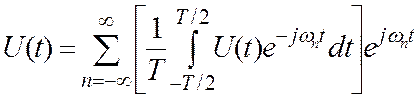 (3.3)
(3.3)
Заметим, что 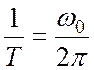
Теперь в формуле (3.3) выполним предельный переход ![]() . При этом:
. При этом:
В результате,
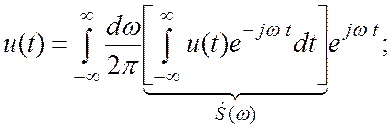 (3.4)
(3.4)
внутренний интеграл в (3.4) обозначим как ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.