Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 14

   Быстрое преобразование Фурье используется также для построения оценок трехмерных спектрограмм. Для этого используется функция SPECGRAM.

    Эти же функции, после дополнения комплексно сопряженными членами, могут быть применены и для расчета спектральной плотности мощности случайных сигналов. Однако, в МАТЛАБЕ есть  набор специальных процедур для такого анализа. Позже мы их  рассмотрим.

   Ниже следует список конкретных заданий, которые необходимо выполнить по ходу работы. Не все они являются обязательными, выполняемый перечень согласуйте с преподавателем.

     Часть 6.1. Расчет и компьютерное моделирование спектров модельных сигналов.

Задание 1. Аналитически рассчитать спектральные функции следующих модельных сигналов:

• Прямоугольного видеоимпульса
• Треугольного импульса
• Экспоненциального импульса.

   Исследуйте амплитудный и фазовый спектр этих сигналов, сравните их особенности.

Задание 2. Изучите встроенную функцию МАТЛАБ pulstran , подготовьте с ее помощью дискретные реализации следующих модельных сигналов:

• Прямоугольного импульса (функция rectpuls)
•  Треугольного сигнала (функция tripuls)

Примечание: с помощью этих функций можно "сконструировать" более сложные сигналы, например, меандр, трапецию и т.п.)

• Функции Дирихле (дает прямоугольный, то есть ограниченный по частоте спектр –функция sinc)
• Гауссов радиоимпульс (функция gauspuls)

   С описанием  этих функций можно ознакомиться по справочной документации МАТЛАБ или по [ 6 ].

   Выполнить Фурье–анализ перечисленных сигналов с помощью функций fft и fftshift, построить соответствующие графики амплитудных и фазовых спектров в области положительных и отрицательных частот. Особое внимание обратить на влияние соотношения длительности импульсов к их периоду повторения, объяснить результат.

Примечание.  Для примера в Приложении 2 приведен

листинг соответствующей  программы для анализа спектра прямоугольного импульса (функция rectpuls).

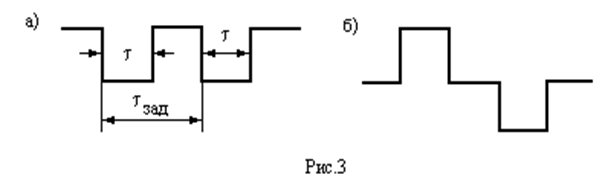
   Задание 3. Рассчитайте спектр пары одинаковых следующих друг за другом,  прямоугольных импульсов с единичной амплитудой и длительностью , запаздывающих друг относительно друга. на время  _зад .      Схематически они представлены на следующем рисунке:

Пусть спектральная плотность одиночного импульса равна .  Как мы уже знаем, спектральная плотность запаздывающего во времени сигнала  связана со спектральной плотностью исходного сигнала через теорему запаздывания:

                                             (6.3)

   Тогда спектральная плотность двух одинаковых, но сдвинутых во времени, сигналов представляется в виде линейной суммы:

                   

   В последней формуле 1 представим в виде:

                             

а экспоненту  , соответственно, в виде произведения .

   Тогда:

         

                                                          (6.4)

Но для одиночного прямоугольного импульса нам  известна.  Учитывая это, можно найти модуль спектральной плотности двух одинаковых сдвинутых прямоугольных импульсов:

     

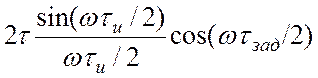
   Отсюда видно, что огибающая спектра двух прямоугольных импульсов приобретает дополнительные нули, определяемые временем задержки .

   В случае, когда второй импульс имеет противоположную полярность по отношению к первому, суммарная спектральная плотность, как нетрудно убедиться, имеет вид:

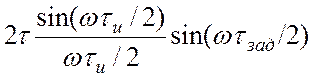                                             (6.5)

и в огибающей спектра опять появляются дополнительные нули. Определить  положение нулей в том и другом случае читатель может самостоятельно.

    Проверьте эти закономерности, сгенерировав соответствующие реализации сдвинутых сигналов и взяв их преобразование Фурье при разных значениях .

   Задание 4. Проведите спектральный анализ отрезка синусоиды, состоящего из нескольких периодов. Проследите, как меняется спектр в зависимости от числа периодов. Очевидно, что этот параметр определяет разрешающую способность Фурье – анализа, если сигнал состоит из нескольких спектральных компонент. Листинг соответствующей программы приведен в Приложении 3.