Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 18

Задание 8. Генератор модельных сигналов в экспериментальной установке замените генератором шума. Запишите реализацию случайного  сигнала с этого генератора (с выхода фильтра). Исследуйте спектр мощности этого сигнала с помощью:

• собственного анализатора спектра системы L-card
• путем расчета усредненной периодограммы этого процесса с помощью функции periodogram пакета МАТЛАБ, а также функции psd. С  синтаксисом этих функций ознакомьтесь по справочной документации пакета.

   Задание 9. Пропустите исходный шум через колебательный контур, придаваемый к установке. Запишите файл, постройте спектр мощности. По нему определите резонансную частоту контура. Постройте функцию автокорреляции процесса с помощью функции xcorr, дайте физическую интерпретацию полученного результата.

   Задание 10. Соберите простейший RC-фильтр, его параметры предварительно согласуйте с преподавателем. По справочной документации МАТЛАБ изучите функции spectrum и etfe. С их помощью исследуйте частотную характеристику фильтра. Для этого сначала запишите реализацию входного сигнала при выполнении условий теоремы Котельникова, затем  переключите АЦП на выход четырехполюсника и запишите выходной сигнал. Размер входного и выходного файлов должен быть одинаков. Эти файлы образуют переменные X и Y для использования в функциях  spectrum  и etfe.

Примечание. Не все задания к данной работе являются обязательными. Часть из них может быть использована при выполнении курсовых работ в течение текущего семестра. Для конкретизации перечня выполняемых заданий обратитесь к преподавателю.

Раздел 7. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Почему простые гармонические сигналы играют особо важную роль в спектральном анализе?

2. Для чего в спектральном анализе детерминированных сигналов вводятся системы ортонормированных функций?

3. Докажите ортонормированность базисных функций гармонического ряда Фурье.

4. Докажите ортонормированность базисных функций комплексного ряда Фурье.

5. Как соотносятся между собой коэффициенты ряда Фурье в комплексной форме для области положительных и отрицательных частот?

6. Как получить физический спектр сигнала из комплексного ряда Фурье?

7. Сформулируйте основные свойства преобразования Фурье.

8. Если сигнал вещественный, какими особенностями будет обладать его прямое преобразование Фурье?

9. Вычислите спектральную функцию последовательности прямоугольных импульсов.

10. Каковы отличия случайных сигналов от детерминированных?

11. Дайте точную формулировку теоремы Котельникова.

12. Что такое спектральная плотность мощности случайного процесса?

13. Сформулируйте теорему Винера – Хинчина.

14. Как рассчитываются спектры дискретных случайных процессов?

15. Какими особенностями обладают оценки спектра мощности случайных процессов?

16. Как повысить надежность оценок спектра мощности случайного процесса?

Приложение 1. НЕКОТОРЫЕ МОДЕЛЬНЫЕ ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

 1.1. Модели детерминированных сигналов. Решение любых физических задач существенно упрощается, если удается найти какое – либо модельное представление реальных сигналов, наблюдаемых в эксперименте.  Заданная аналитически модель u(t) (детерминированная, определенная в любой момент времени), становится  математической моделью сигнала, не связанной с его физической сущностью и удобной для изучения. Разумеется, такая модель должна адекватно описывать главные особенности реального сигнала. Таких моделей существует множество, ниже мы опишем одни из самых употребительных. Одна из самых основных моделей – гармонический сигнал, о котором говорилось выше. Кроме того, можно указать ещё  ряд распространенных моделей:

• гармонический сигнал конечной длительности (с ограниченным числом периодов) :

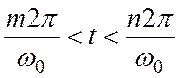              .                                      (1.1)

  Здесь m b n – целые числа.