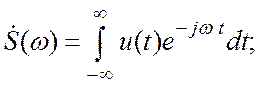Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 6

                                                                                (3.5)

Это так называемое  прямое преобразование Фурье. Зная  , можно найти исходный сигнал:

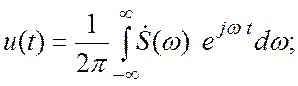                                                                          (3.6)

Формула (4.6) носит название обратного преобразования Фурье. 

   Преобразования (3.5) и (3.6) играют фундаментальную роль в теории сигналов. Функция  называется спектральной плотностью сигнала.   В литературе   называют также спектральной функцией сигнала. Спектральную функцию (3.5) можно представить в показательной форме:

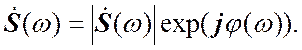                                              (3.7)

Здесь

                                       

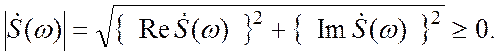
есть амплитудная спектральная функция (часто, несмотря на неточность термина, говорят «амплитудный спектр»), а

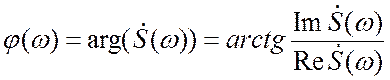                                                        (3.8)

– есть фазовая спектральная функция («фазовый спектр»). Амплитудный спектр 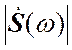 является четной, а фазовый спектр  нечетной функциями . Принимая это во внимание и подставляя (3.7) в (3.6), получим соотношение

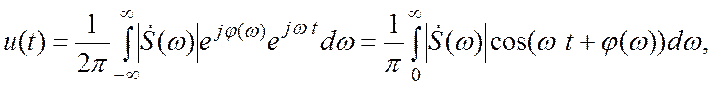
иллюстрирующее «физический смысл» спектральной функции: сигнал  представляется в виде суммы бесконечно большого числа гармонических составляющих с бесконечно малыми амплитудами 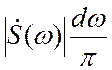, непрерывно заполняющих интервал частот от нуля до . Начальные фазы этих составляющих заданы функцией , а частотная зависимость «плотности» бесконечно малых амплитуд описывается функцией .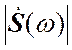

   Размерность спектральной функции  есть размерность сигнала, умноженная на время; так что, если размерность  - вольты, то .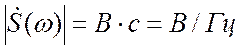

   Поскольку преобразование Фурье – одно из фундаментальных понятий теории сигналов, подробно рассмотрим его свойства.

Свойства преобразований Фурье.

   1.«Площадь» сигнала. Положив в соотношении (3.5) , получим

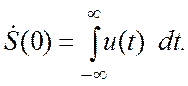                                                                                       (3.9)

Значение  численно равно «площади» сигнала в системе координат «время—сигнал».

  2. Спектральная плотность суммы сигналов (линейность преобразования Фурье). Пусть  – сигналы со спектральными функциями , соответственно. Тогда сигналу соответствует преобразование Фурье в виде:

                                                  (3.10)

Доказательство предоставляется читателю сделать самостоятельно.

   3. Сдвиг сигнала во времени (теорема запаздывания). Пусть сигналу соответствует спектральная функция . Найдем преобразование Фурье сдвинутого во времени сигнала :

=

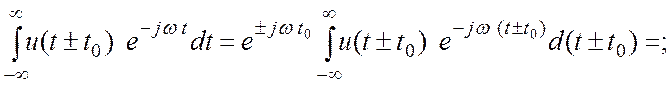
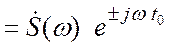                        (3.11)

При сдвиге сигнала на временной интервал  амплитудный спектр сигнала не изменяется, в фазовом спектре сигнала появляется дополнительная компонента . Множитель  называют оператором задержки сигнала.

   Пример. Спектральная функция задержанного, т. е. сдвинутого по оси абсцисс на время τ_u/2  видеоимпульса (исходный график несдвинутого сигнала см. Рис.1.4 Приложения 1):

                   

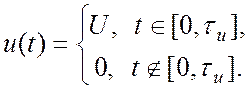
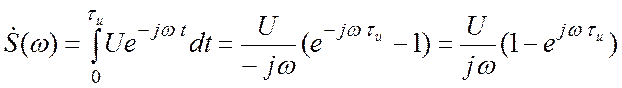
В скобках единицу представим как  , второй член представим как произведение двух экспонент с половинным показателем, тогда приходим к выражению:

             

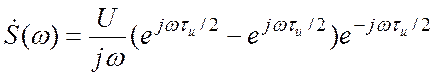
   Это выражение домножим и разделим на , в числителе получаем формулу Эйлера. Окончательно:

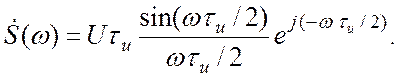                  (3.12)

что соответствует формуле (3.11) –. спектральная функция прямоугольного импульса домножается на экспоненту , отражающую сдвиг импульса на  .

   Изменение масштаба оси времени. Найдем преобразование Фурье для сигнала с измененным по времени масштабом :

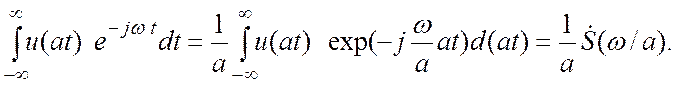
При  аналогичным образом получим

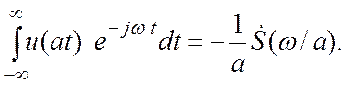
Объединение обоих случаев дает формулу

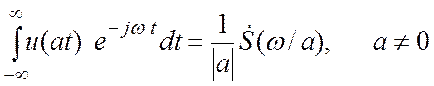
Сжатию (растяжению) сигнала во времени отвечает растяжение (сжатие) спектральной функции по оси частот.

   Дифференцирование сигнала (спектральная функция производной).

Пусть сигналу  соответствует спектральная функция. Будем искать спектральную функцию сигнала. Воспользуемся обратным преобразованием Фурье:

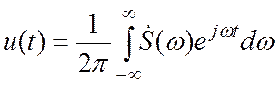
и продифференцируем по времени левую и правую часть этого выражения. Получим:

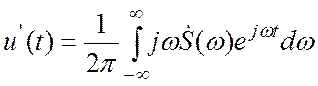                                                                               (3.13)