Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 11

   В Разделе 4 отмечалось, что экспериментальные реализации любых (и детерминированных и случайных) процессов в современном эксперименте получаются с помощью ЭВМ. Эти реализации всегда обладают конечной длительностью, которую можно задать количеством отсчетов умноженным на частоту квантования сигналов  .

При переходе к дискретным реализациям сигналов ограниченной длительности формула (5.1) приобретает вид:

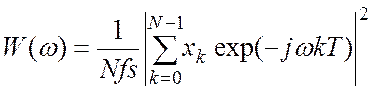                                                                                         (5.4)

Формула (5.4) дает так называемую периодограмму дискретного сигнала. Это оценка его спектральной плотности мощности, полученная по отсчетам одной реализации, естественно, не путем взятия предела, как в ф-ле (5.1), а усреднением конечного числа слагаемых.

   Следует отметить, что ф-ла (5.4) наиболее часто используется при анализе спектров случайных процессов, поскольку имеется мощный современный аппарат вычисления преобразования Фурье – так называемое быстрое преобразование Фурье [ 6 ]. Применение теоремы Винера–Хинчина в современной литературе встречается реже.

   Главная проблема, возникающая при расчетах по ф-ле (5.4) заключается в том, что получаемая оценка не является состоятельной, это показано в работе [ 10 ]. Понятие состоятельности оценки заключается в том, что её дисперсия должна стремиться к нулю при увеличении интервала анализа. У периодограммы (5.4) дисперсия оценки  сравнима с квадратом её математического ожидания, что совершенно недопустимо.

   Для иллюстрации этой закономерности на Рис.5.1 приведен график некоторого исходного случайного процесса и его периодограмма.  Очевидно, что периодограмма – это тоже случайный процесс, но в частотной области. Заметим, что если увеличивать число используемых отсчетов, значения периодограммы будут  все быстрее флуктуировать.

  

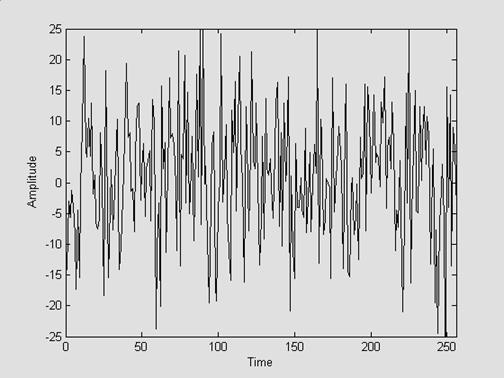
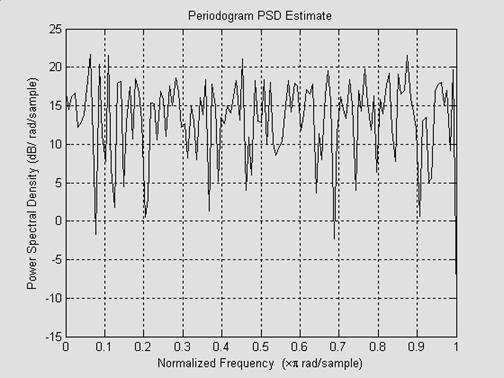
Рис.5.1. Случайный процесс и его периодограмма.

                       Рис.5.1. Исходный случайный процесс и его периодограмма.

   Для уменьшения  изрезанности периодограммы необходимо применить какое-либо усреднение. Даньелл  [ 6 ] предложил сглаживать быстрые флуктуации выборочного спектра путем усреднения по соседним частотам спектра. Данный метод, называемый  периодограммой Даньелла, сводится к вычислению свертки периодограммы с некоторой  сглаживающей функцией. В методе Бартлетта [ 6 ]  анализируемый сигнал делится на неперекрывающиеся сегменты, для каждого сегмента вычисляется периодограмма и затем эти периодограммы усредняются. Если корреляционная функция сигнала на длительности сегмента затухает до пренебрежимо малых значений, то периодограммы отдельных сегментов можно считать независими. В этом случае дисперсия периодограммы Бартлетта обратно пропорциональна числу используемых сегментов, однако с ростом числа сегментов падает спектральное разрешение (за счет того, что сегменты становятся короче)  [ 10 ].

   Уэлч внес в метод Бартлетта два усовершенствования: использование весовой функции и разбиение сигнала на перекрывающиеся фрагменты.  Перекрытие сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки. Вычисления при использовании метода Уэлча (он называется еще методом усреднения модифицированных периодограмм — averaged modified periodogram) организуются следующим образом:

1.  Вектор отсчетов сигнала делится на перекрывающиеся сегменты. Как правило, на практике используется перекрытие на 50 %, хотя это не всегда оптимально. Строго говоря, оптимальная степень перекрытия зависит от используемой весовой функции. Каждый сегмент умножается на используемую весовую функцию.

2.  Для взвешенных сегментов вычисляются модифицированные периодограммы.

3.  Периодограммы всех сегментов усредняются

.

   Также как для периодограммы Бартлетта, дисперсия оценки, получаемой методом Уэлча, уменьшается примерно пропорционально числу сегментов. Благодаря перекрытию в методе Уэлча используется больше сегментов, поэтому дисперсия оценки спектра мощности оказывается меньше, чем для метода Бартлетта. Метод Уэлча, согласно [ 6 ], является сейчас наиболее популярным периодограммным методом спектрального анализа случайных процессов.