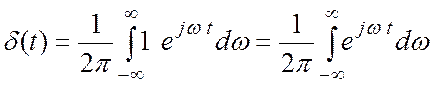Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 8

.

Из последней формулы следует кстати, что в показателе экспоненты может стоять любой знак, плюс или минус. Это видно из следующего выражения:

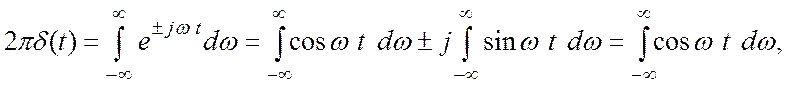          (3.23)

мнимый член в этой формуле равен нулю поскольку нечетная функция  интегрируется в симметричных пределах.

   Таким образом, мы имеем ещё одно определение   – функции:

 

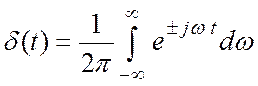                                                                                                                       (3.24)

Воспользуемся известным свойством симметрии преобразования Фурье относительно переменных  и   и  в (4.24) поменяем их местами:

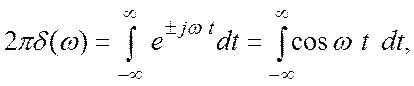                                                  (3.25)

Это выражение дает определение  – функции в частотной области:

 

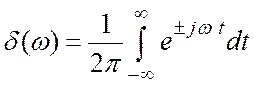                                                                                                                      (3.26)

Если  – функция сдвигается во времени на , её преобразование Фурье по теореме запаздывания :

                      

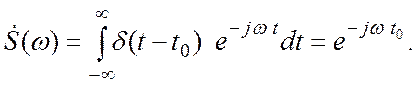
   Амплитудный спектр сдвинутой во времени  – функции не изменяется, фазовый спектр приобретает дополнительное слагаемое .

Преобразование Фурье некоторых неинтегрируемых абсолютно сигналов.

   Математические модели некоторых широко используемых в теоретической радиотехнике сигналов не удовлетворяют условию абсолютной интегрируемости . Следовательно, преобразование Фурье в обычном виде к ним неприменимо.

   Распространить методы преобразования Фурье на сигналы такого рода позволяет использование функции Дирака спектральная характеристика которой была определена ранее.

   Спектральная функция постоянного во времени сигнала. Пусть U=const, тогда спектральная функция  постоянного во времени (абсолютно неинтегрируемого) сигнала

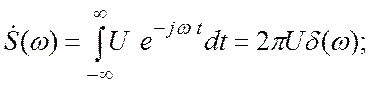                                           (3.27)

Физический смысл этого результата очевиден — постоянному во времени сигналу соответствует спектр, состоящий  из единственной составляющей на нулевой частоте —.

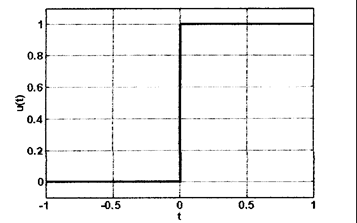
   Преобразование Фурье функции Хевисайда. График функции Хевисайда (единичной ступеньки) показан ниже:

 

Формально эта функция не является абсолютно интегрируемой. Умножим её на некоторый "гасящий "множитель  , вычислим спектральную функцию, а потом сделаем предельный переход :

       =

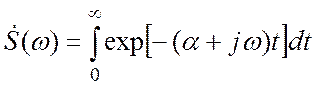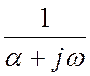
Переходя к пределу  получаем . В литературе [ 2 ] показано, что такой предельный переход справедлив на всех частотах, кроме . Согласно [ 2 ] спектральная функция единичной ступеньки равна

                                            

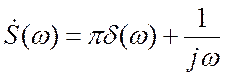
   Преобразование Фурье гармонического сигнала. Гармонический сигнал  также является неинтегрируемой абсолютно функцией. Вычислим его спектральную функцию используя формулу Эйлера и представление – функции.

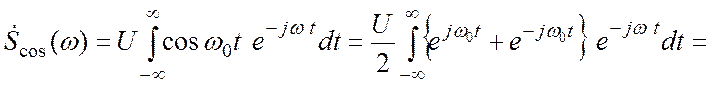
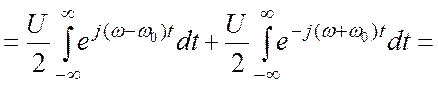
                                                                  (3.40)

   Гармоническому колебанию с конечной амплитудой соответствует спектральная функция с -особенностями в точках  частотной оси. Положив в этой формуле  как частный случай получим уже известный результат (3.27) — спектр постоянного во времени сигнала.

   Приведенные   формулы в некоторых случаях позволяют заметно упростить вычисления. Рассмотрим, например, сигнал, представленный как произведение двух функций, каким, по существу, является радиосигнал с медленно меняющейся огибающей (в масштабе времени ) и гармоническим заполнением на частоте с медленно меняющейся фазой :

                                      

Спектральная функция произведения сигналов  рассматривалась выше. Обозначим через  спектр огибающей,  спектр  гармонической функции  и подставим эти спектры в формулу (3.18)  Тогда спектр радиосигнала представится в виде:

 

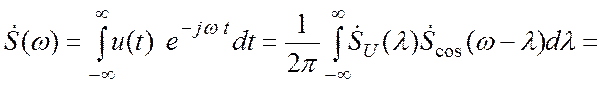
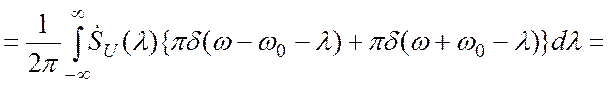
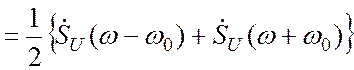                               (3.41)

Здесь использовано фильтрующее свойство дельта-функции. Аргументами, при которых существуют  и   являются, соответственно,  и Из формулы (3.41) вытекает, что спектр радиосигнала состоит из спектра огибающей , который делится  пополам и разносится по частотной шкале на частоты +          и .