Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 10

Интеграл в (5.9) легко берется, и окончательно выражение это выражение приводится к виду:

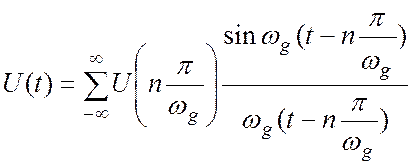                                                                  (4.10)

     Это и есть теорема Котельникова, она связывает значения непрерывного сигнала  c его значениями, взятыми в дискретные моменты времени. Удобнее сформулировать ее не в терминах круговых частот , а в обычных частотах , измеряемых в герцах. Учитывая, что получаем:

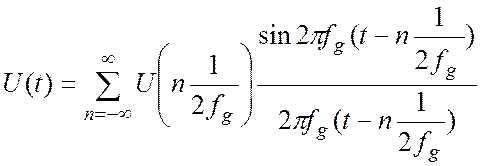                                                              (4.11)

      В литературе выражение   носит название частоты Найквиста. Используя его, окончательно получаем:

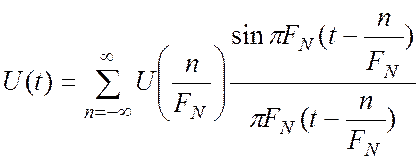                                                                (4.12)

   В этом виде теорема Котельникова чаще всего приводится в литературе. Проделанные вычисления не содержат каких-либо приближений, поэтому исходный сигнал и его дискретная  реализация в моменты времени, кратные 1/F_N, совпадают точно.

Ряд 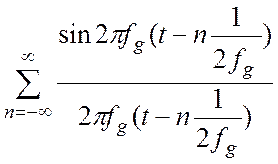   называется в литературе базисом Котельникова. Можно показать, что любые функции из этого ряда образуют ортонормированный базис. Таким образом, формула (4.12) есть разложение сигнала по базису Котельникова.

   Поясним сказанное примером. На Рис.4.3 приведен график некоторого исходного сигнала . Проквантуем его  по времени с   (время условное) и затем восстановим, пользуясь теоремой Котельникова. Восстановленный сигнал  показан на Рис.4.4. Там же пунктиром нанесены графики базиса Котельникова, относящиеся к последовательным моментам времени. Видно, что в моменты  сигналы  и  совпадают.

 

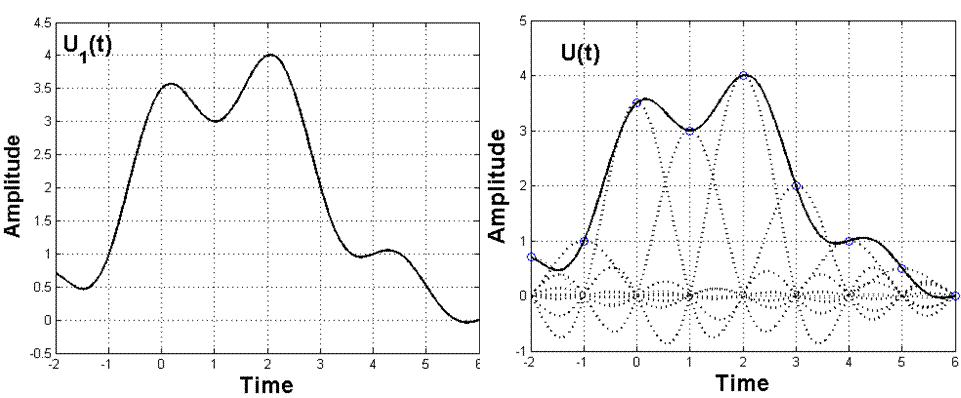               Рис.4.3. Исходный сигнал                     Рис.4.4. Восстановленный сигнал

   Можно показать, что если частота квантования сигнала превышает , то восстановление исходной аналоговой реализации сигнала также возможно. Если же частота квантования меньше , то условия теоремы Котельникова нарушаются, восстановление исходного сигнала будет сопровождаться искажениями.

Раздел 5. СПЕКТРАЛЬНЫЙ АНАЛИЗ СЛУЧАЙНЫХ СИГНАЛОВ

 Для случайных сигналов изложенные выше методы спектрального анализа  неприменимы. Причины этого обсуждаются в описании Лабораторной работы "Автоматизированные измерения и моделирование  случайных процессов", а также в [ 6, 7 ,8 ]. Там же даются основные сведения из теории случайных процессов, поэтому здесь мы будем пользоваться уже готовыми результатами, вытекающими, в частности,  из материала упомянутой работы.

   Ограничимся рассмотрением стационарных эргодических процессов , для которых получение усредненных статистических оценок каких либо параметров возможно по одной, достаточно протяженной реализации (а не по ансамблю реализаций).

   Нам понадобятся следующие определения:

Спектральная плотность мощности случайного процесса:

 

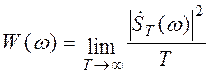                                                                                     (5.1)

Автокорреляционная функция случайного процесса:

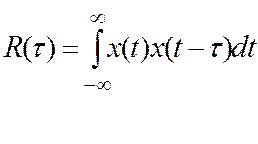(5.2)

Связь между спектральной плотностью мощности и автокорреляционной функцией дается теоремой Винера Хинчина.

Теорема Винера–Хинчина:

                   

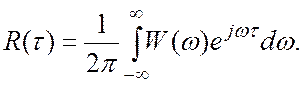
                                                                                                                                                    (5.3)

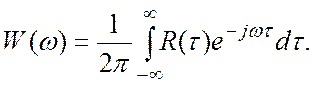
   То есть автокорреляционная функция и спектральная плотность мощности связаны парой преобразований Фурье.

   Все методы спектрального анализа случайных процессов в литературе делятся на непараметрические и параметрические [ 6 ]. Непараметрические методы используют только информацию, заключенную в самих отсчетах сигнала, без каких-либо дополнительных предположений. Параметрические – предполагают наличие какой-нибудь предварительной модели сигнала, например, наличие спектральной компоненты в шуме и ставится задача определить её амплитуду.

   К непараметрическим методам принадлежат разновидности анализа, основанные на преобразовании Фурье. Это объясняет их широкое применение при анализе случайных процессов. Параметрические методы в этой работе мы рассматривать не будем.