Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 12

Что касается весовых функций, используемых в методе Уэлча, то они реализованы в виде так называемых окон. Остановимся на этом вопросе подробнее.

Оценка спектральной плотности мощности (5.4) ведется по ограниченному числу отсчетов процесса . Можно трактовать это так, что некоторая исходная реализация с бесконечным числом отсчетов, множится на дискретную функцию времени , "вырезающую" из бесконечной реализации ровно  отсчетов [ 13 ]:

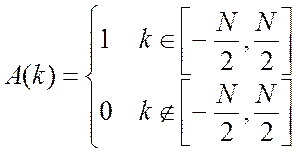                                                                              (5.5)

  Говорят, что функция  – это временное окно, в данном случае из (5.5) следует, что оно прямоугольное, его длина равна . Фактически мы имеем дело со сверткой исходного сигнала и функции окна. Выше было показано, что свертка сигналов дает в частотной области произведение спектральных функций сигнала и окна. Спектральная функция окна в данном случае нам хорошо известна, она представлена на Рис.2.3. Она имеет характерные выбросы вокруг главного лепестка, они могут  давать ложные компоненты в оценке .

   Чтобы устранить эти явления, выбираются другие функции окон. Они должны удовлетворять следующим условиям [ 13 ]:

·  частотное окно должно иметь возможно более узкий центральный пик

·  число боковых выбросов в спектре окна должно быть небольшим, а сами выбросы –минимальными

·  отрицательные выбросы должны отсутствовать.

Пакет МАТЛАБ содержит целый ряд  оконных функций, отвечающих этим требованиям. Они названы по именам исследователей, в своё время их предложивших.  Они задаются во временной области и множатся на текущие значения сигнала перед вычислением спектров.  С их помощью и реализуется метод модифицированных периодограмм Уэлча, о котором говорилось выше. В качестве примера рассмотрим окно Хемминга [ 6 ], оно весьма часто употребляется при спектральном анализе.  Его аналитический вид дается формулой:

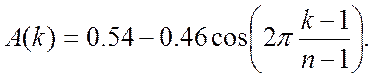
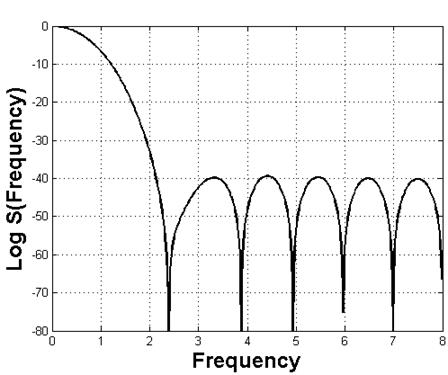
   Графическое изображение этого окна представлено на Рис.5.2.  Оно построено для 16 дискретных отсчетов сигнала. На Рис.5.3 показана его спектральная функция для положительных частот в логарифмическом масштабе.

 

                 Рис.5.2. Окно Хемминга                 Рис.5.3. Амплитудный спектр окна Хемминга

   Эта функция удовлетворяет сформулированным выше требованиям, спектр её имеет один лепесток, амплитуды остальных выбросов подавлены до уровня – 40 децибел (в 100 раз).

   Кроме окна Хемминга в пакете МАТЛАБ имеется 15 других  оконных функций, их правильный выбор зависит от характера случайного процесса и длины его реализации. Подробности работы с различными окнами можно почерпнуть из [ 10 – 13 ].

   Что касается программной реализации метода Уэлча, то пакет МАТЛАБ имеет в своем составе готовый набор процедур для расчета  модифицированных периодограмм, он описан в[ 6 ]. В качестве примера использования метода Уэлча рассмотрим Рис.5.4, где представлена усредненная периодограмма, та же, что и на Рис.5.1.

 

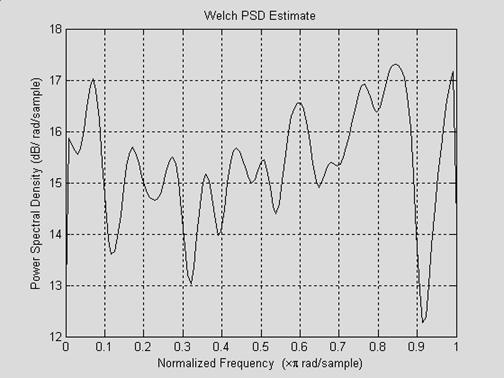                   Рис.5.4. Периодограмма, усредненная по методу Уэлча

На усредненной периодограмме начинают вырисовываться квазипериодические детали спектра мощности процесса, которые невозможно было увидеть на Рис.5.1. В практической части нашей лабораторной работы к методу Уэлча мы ещё вернемся.

В заключение данного Раздела укажем на ещё одну интересную область применения аппарата спектрального анализа случайных процессов. Пусть имеется некоторая линейная система с одним входом и одним выходом. Пусть также на её входе действует стационарный эргодический процесс  со спектральной плотностью , тогда на выходе появляется процесс  со спектральной плотностью .  Эти процессы связаны между собой функцией взаимной корреляции :

                                                                                                                    

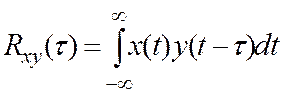
                                                                                                                      (5.6)