Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 3

·  на интервале Т   функция  является однозначной, либо она имеет конечное число разрывов первого рода

·   обладает конечным числом максимумов и минимумов

Нетрудно показать, что любой физически реализуемый сигнал этим условиям удовлетворяет. Действительно, он однозначен, разрывов  вообще не может иметь, т.к. разрыв предполагает бесконечную мощность источника для его реализации, и, наконец, он не может иметь бесконечное число максимумов и минимумов, иначе его частота была бы бесконечной.

   Если условия Дирихле для f(x)  выполняются, то эта функция может быть представлена в виде суммы ряда

                                                                                                          (1.6)

Для нахождения коэффициентов разложения умножим обе части выражения  (1.6) на  и проинтегрируем в пределах а, b. Все слагаемые вида 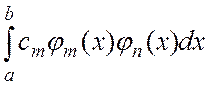 при  обращаются в нуль в силу ортогональности функций  и . В правой части остается одно слагаемое 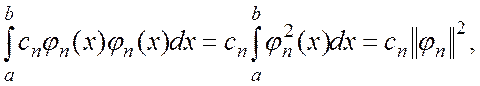что позволяет написать

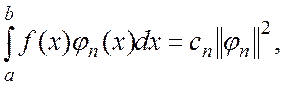
Откуда следует

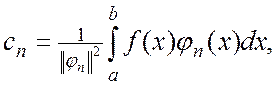                                                                                      (1.7)

Ряд (1.6), в котором коэффициенты с_п определены по формуле (1.7), называется обобщенным рядом Фурье по данной системе . Обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций и при фиксированном числе слагаемых ряда (1.6) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции . Это означает, что среднеквадратическая ошибка, под которой подразумевается величина

                          

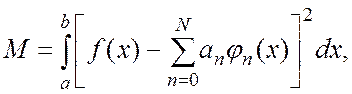
достигает минимума, когда коэффициенты ряда . 

   Действительно, подставив в предыдущее выражение  и использовав равенства (1.2), (1.5) и (1.7), получим

                            

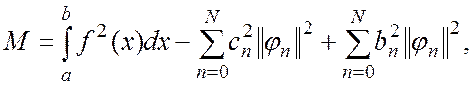
Отсюда следует, что достигает минимума при  = 0,   т. е, при . Таким образом,

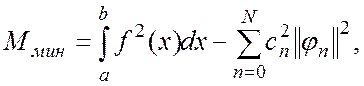                                               (1.8)

Так как величина

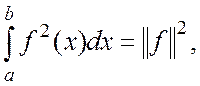
является квадратом нормы функции f(х), а, то на основании (1.8) можно написать следующее неравенство:

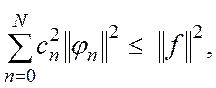                                                                                                                                                               (1.9)

Это основное неравенство, назывемое неравенcтвом Бесселя, справедливо для любой ортогональной системы.

Ортогональная система называется полной, если увеличением числа членов в ряде среднеквадратическую ошибку М можно сделать сколь угодно малой.

Условие полноты можно записать в виде соотношения

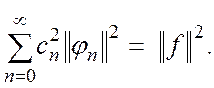                                                                                    (1.10)

Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди разнообразных задач, требующих разложения сложного сигнала, наиболее важными являются:

·  точное разложение на  ортогональные функции,

·  аппроксимация сигналов, процессов или характеристик, когда требуется свести к минимуму число членов ряда (при заданной допустимой погрешности).

Для решения  первой  задачи наибольшее распространение получила ортогональная система основных тригонометрических функций — синусов и косинусов, на этом мы подробно остановимся в следующем разделе. Причин этому несколько. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через любую линейную цепь (с постоянными параметрами), изменяется лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи. По этим, а также и некоторым другим причинам гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

Помимо гармонического базиса, в современных системах обработки сигналов получили применение и другие  системы ортонормированных функций – Уолша, Хаара, Виленкина-Кристенсена и др.[ 3 ].  Несколько первых функций  базиса Уолша представлены на Рис.1.1