Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 2

 Предполагается, что читатель знаком с основными приемами работы в этом пакете.  Программы расчетов и различные дополнения будут отнесены в Приложения к работе.

Изложение начнем с двух примеров. На Рис.1  приведены модельные осциллограммы  детерминированного сигнала (периодической последовательности треугольных импульсов) и широкополосного нормального шума. Видна качественная разница между ними. Если значения детерминированного сигнала в любой момент времени могут быть предсказаны, то текущие значения случайного сигнала испытывают хаотические флуктуации и заранее непредсказуемы.

 

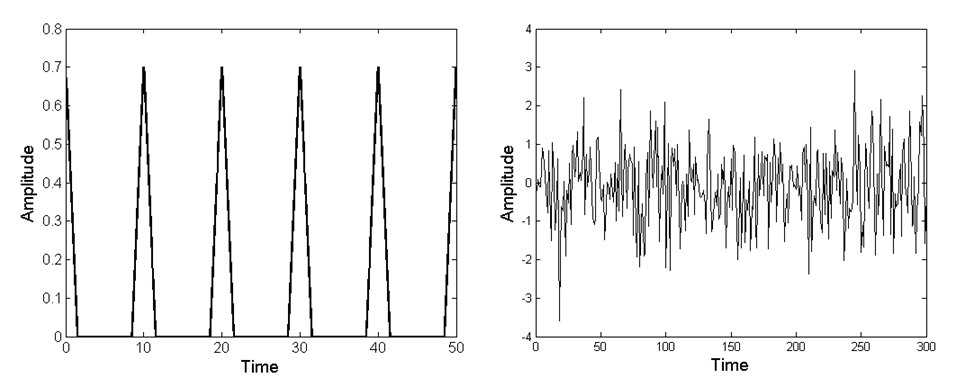Рис.1. Осциллограммы детерминированного и случайного сигналов.

Для многих разновидностей детерминированных сигналов можно ввести модели, описывающие их поведение во времени. Некоторые такие  модели рассмотрены в Приложении 1. Там же описаны так называемые тестовые сигналы, которые часто применяются при исследовании электрических цепей – это функция Хевисайда и дельта–функция. Более подробно с этими сигналами можно ознакомиться в [ 2 ], [ 4 ].

Детерминированные сигналы можно, в свою очередь, классифицировать по ряду признаков. Например, их можно  подразделить на периодические и непериодические. Периодическим называется любой сигнал, для которого выполняется условие , где период  является конечным отрезком времени, а  – любое целое число.

Простейшим периодическим детерминированным сигналом является гармоническое колебание , определяемое законом:

                                         

где   – амплитуда, – частота,  – начальная фаза, –<   <  .                                

    Замечательным свойством такого сигнала является то, что любой физически реализуемый сложный периодический сигнал можно представить в виде суммы гармонических колебаний со своими амплитудами, фазами и частотами, кратными основной частоте .

Такое представление соответствует так называемому гармоническому ряду Фурье. Следует сразу сказать, что гармонический ряд Фурье далеко не единственная форма представления сложных периодических сигналов. Сигнал можно разложить на составные части пользуясь и другими, не обязательно гармоническими функциями. Однако все они должны удовлетворять некоторым общим закономерностям. Рассмотрим этот вопрос подробнее.

Раздел 1. .РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА ПО

ОРТОГОНАЛЬНЫМ СИСТЕМАМ ФУНКЦИЙ

    В данном разделе мы рассмотрим основные теоретические предпосылки изучения спектров сигналов путем их разложения  по так называемым ортогональным системам функций. Независимо от конкретного вида этих функций, математический аппарат такого анализа стандартизован. Поэтому рассмотрим его в общем виде.   Предположим, что математическая модель сложного сигнала известна и определяется функцией  Заметим, что  – это не обязательно время,  может быть любым аргументом. Разложение  производится по различным ортогональным системам функций. Такие разложения широко применяются в физике и математике. Рассмотрим основные определения, относящиеся к свойствам ортогональных систем [ 2 ].      

   Бесконечная система действительных функций

                                                                     (1.1)

называется ортогональной на отрезке [a, b], если

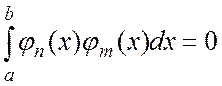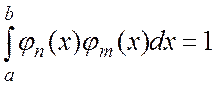    при  

                                            при                                (1.2)

При этом предполагается, что

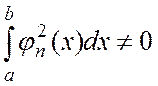                                                                                                          (1.3)

т. е. что никакая из функций рассматриваемой системы (1.1) не равна тождественно нулю.

Условие (1.2) выражает  попарную ортогональность функций системы (1.1). Величина

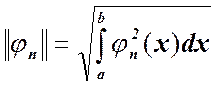                      (1.4)

называется нормой функций .

Функция , для которой выполняется условие

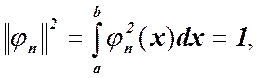                           (1.5)

называется нормированной функцией, а система нормированных функций  в которой каждые две различные функции взаимно ортогональны, называется     о р т о н о р мированной системой. По такой системе может быть разложен  периодический сигнал f(x) для которого интервал  соответствует его периоду Т , а сам сигнал удовлетворяет так называемым условиям Дирихле  [ 2 ]: