Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 4

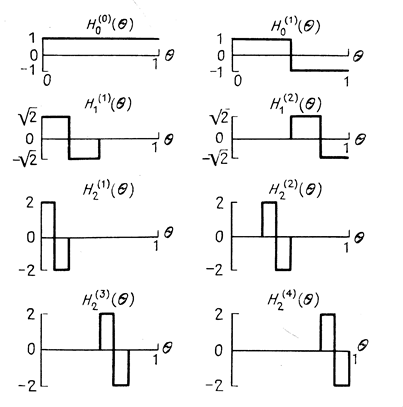
Рис.1.1 Несколько первых функций базиса Уолша.

   Они зависят от параметра который меняется в диапазоне .  Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно. Базис Уолша широко применяется при разложении сигналов в двоичной форме представления, он обеспечивает высокую скорость вычислений на ЭВМ.

   При второй постановке задачи — приближенном разложении функций – применяются разнообразные ортогональные системы математических функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра и многие другие. Такие задачи широко представлены в курсах математики, но они  выходят за рамки данной лабораторной работы.

Раздел 2. .РАЗЛОЖЕНИЕ ПЕРИОДИЧЕСКИХ СИГНАЛОВ В ТРИГОНОМЕТРИЧЕСКИЙ РЯД ФУРЬЕ

 Вернемсяк периодическим сигналам, зависящим от времени u(t). Выше отмечалось, что для возможности разложения u(t) в ряд Фурье должны выполняться условия Дирихле. Отмечалось также, что любой физически реализуемый сигнал таким условиям удовлетворяет. Пусть  исходный сигнал повторяется с периодом T, как показано на Рис. 2.1:

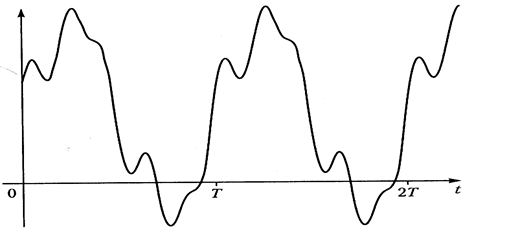                                     u(t)

Рис.2.1

                                   Рис.2.1. Сложный периодический сигнал

Система действительных функций (1.1)      задается   следующим образом:

    

   …..

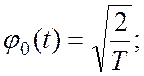
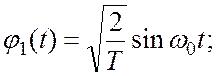
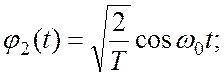
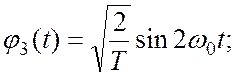
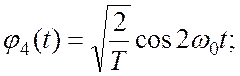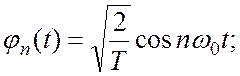
где 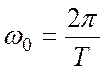.    Тогда разложение для u(t) приобретает вид:

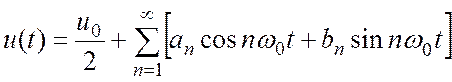                                (2.1)

где

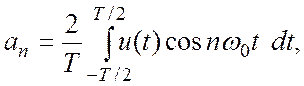
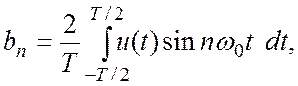          (2.2)

член   описывает постоянную составляющую сигнала:

                                                      

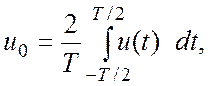
   Ряд (2.1) можно переписать в более компактном виде:

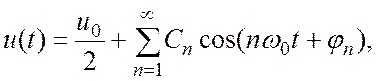                                                  (2.3)    

где

        

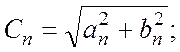
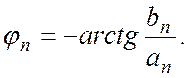
Форма записи (2.3) обычно называется рядом Фурье в вещественной форме. Совокупность образует амплитудный спектр, а совокупность ,  соответственно,  фазовый спектр периодического сигнала. Разложения (2.1) и (2.3) широко используются на практике. Однако более удобной оказывается комплексная форма записи ряда Фурье.

   Комплексная форма ряда Фурье. Воспользовавшись формулами Эйлера:

 

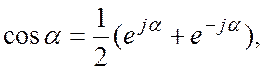
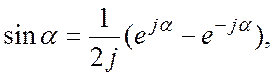
ряд (2.3) можно переписать в виде:

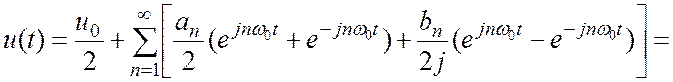
                                                                                                                                    (2.4)

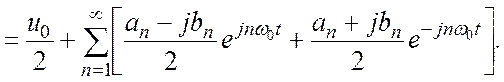
   Введем комплексные амплитуды:

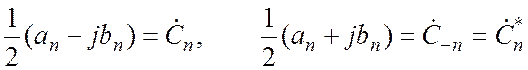
и "отрицательные" частоты : тогда ряд (2.4) запишется в виде:

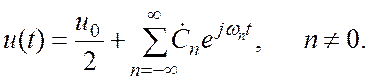
   Это представление называют комплексной формой ряда Фурье. Если дополнительно ввести обозначение , то ряд Фурье  в комплексной форме можно записать лаконичнее:

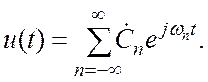                                                 (2.5)

Для вычисления конкретных значений коэффициентов  воспользуемся тем обстоятельством, что базис экспоненциальных функций ,  образует ортонормированный базис. Действительно, как легко убедиться

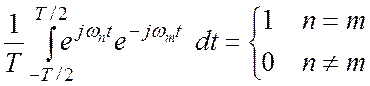          (2.6)

   Умножим обе части (2.5) на  и проинтегрируем по периоду. В силу (2.6) справа останется только коэффициент, для которого m=n. Следовательно,

 

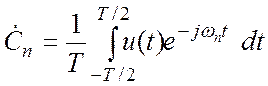                           (2.7)

   Эти коэффициенты  образуют дискретный комплексный спектр периодического сигнала, определённый на всех частотах ω_n,=n₀ ,n=0, ±1, ±2,…. 

Значения модулей  дают амплитудный спектр, – его фазовый спектр. Заметим, что в приведенных формулах появились отрицательные частоты. Физического смысла они не имеют, но их употребление сильно упрощает вычисления.

   Определим коэффициенты  для одного из самых важных модельных сигналов – последовательности прямоугольных импульсов с амплитудой ,  длительностью , следующих с периодом  Т: Этот сигнал показан на Рис.2.2.   Вычисления дают значения:

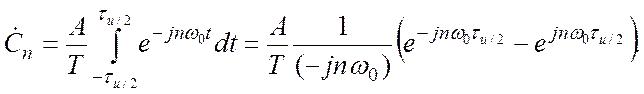                         (2.8)

 Умножим числитель и знаменатель (2.8) на  и на – 1. Применяя формулу Эйлера получим: 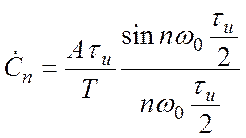                                                                    (2.9)

 

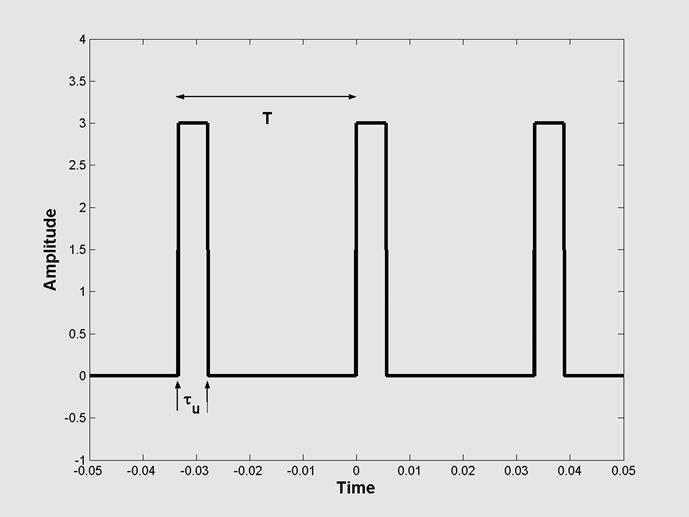Рис.2.2. Последовательность прямоугольных импульсов

   Значения модулей  коэффициентов разложения (2.9)  =  графически показаны на Рис.2.3 в условном масштабе,  они дают спектр амплитуд  членов ряда Фурье.