Методы определения спектральных характеристик электрических сигналов: Учебно методическое пособие, страница 7

   Под интегралом стоит произведение  – спектральная функция производной сигнала. Обратное Фурье преобразование от неё дает . Таким образом, множитель есть оператор дифференцирования в частотной области. При дифференцировании происходит относительный подъем амплитудного спектра сигнала в области верхних частот.

   Интегрирование сигнала (спектральная функция интеграла). Пусть сигнал представлен в виде интеграла :

                                                          

Снова воспользуемся обратным преобразованием Фурье:

                                          

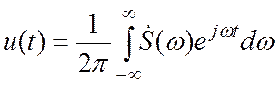
и проинтегрируем его левую и правую часть. Получаем:

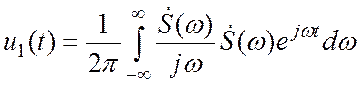                                                 (3.14)

отсюда следует, что спектральная функция проинтегрированного сигнала есть спектральная функция исходного сигнала делённая на .

   В математической литературе доказывается, что соотношение (3.14.) справедливо только для сигналов, отвечающих условию

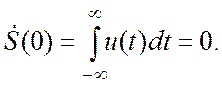                                   (3.15)

 (сигналы с «нулевой площадью»). Если условие (3.14) не выполняется, то спектральную функцию сигнала  следует записывать в виде:

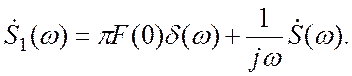                                                      (3.16

Множитель  называют оператором интегрирования в частотной области. При интегрировании происходит относительный подъем амплитудного спектра сигнала в области нижних частот.

   Спектральная функция произведения сигналов (теорема о свертке спектров).

   Пусть рассматриваемый сигнал является произведением двух функций времени:

                                 

   Используя прямое преобразование Фурье найдем спектральную функцию этого произведения:

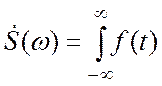
                                                                       3.17

   Пусть  также сигналам и  соответствуют их спектральные функции  и  соответственно. Тогда каждую из функций и  можно представить через обратное преобразование Фурье:

        ;         

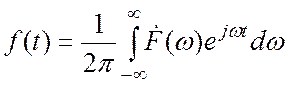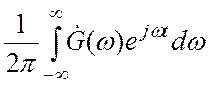
   Подставляя в (3.17) второй из этих интегралов и заменяя в нем переменную интегрирования  , получаем

                         

                                    

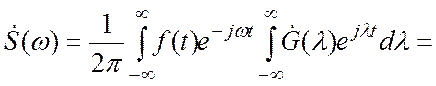
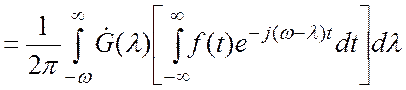
   Заключенный в квадратные скобки интеграл представляет собой спектральную плотность функции  при частоте  , т.е. . Следовательно,

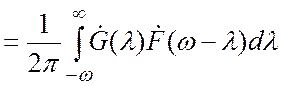                                                                        (3.18)

   Итак, спектральная функция произведения сигналов есть  свертка  их спектральных функций с коэффициентом 1/(2π).

   Из выражений (3.17) и (3.18) в частном случае вытекает следующее равенство:

                                         

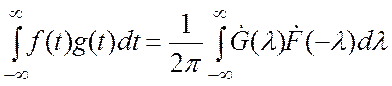
   Заменяя в последнем выражении  на , получаем: 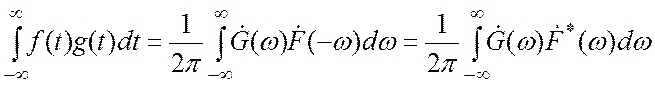                           (3.19)

Здесь учтено соотношение     Выражение (3.19) носит название теоремы Релея.

   Равенство Парсеваля. При  из теоремы Рэлея следует равенство Парсеваля:

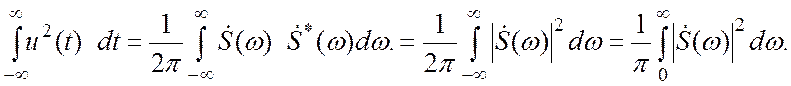       (3. 20)

Формула (3.20) имеет ясный физический смысл .   Интеграл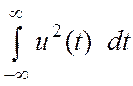  – это энергия сигнала, рассеиваемая на сопротивлении в 1 ом. Её можно найти, проинтегрировав  квадрат спектральной плотности сигнала.

Спектр свертки сигналов. Пусть  и  – сигналы со спектральными функциями  и  соответственно. Будем искать спектральную функцию свертки  этих сигналов. Функция  есть обратное преобразование Фурье спектральной функции :

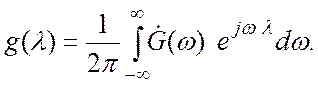
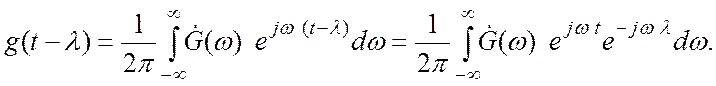
Таким образом

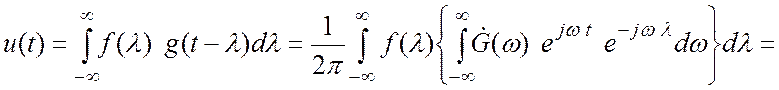
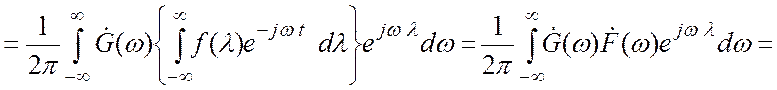
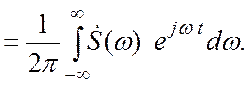
Таким образом, показано (изменением не влияющего на результат порядка интегрирования в двойном интеграле), что спектральная функция свертки сигналов есть произведение их спектральных функций:

                      (3.21)

Это важнейшее соотношение, связывающее, в частности, временной и спектральный подходы к анализу преобразований сигналов в линейных цепях.

Преобразование Фурье некоторых сигналов.

   Спектр дельта-функции Дирака. Эта функция  описана в Приложении  1 к работе.      Воспользуемся фильтрующим свойствам – функции и будем искать ее спектр:

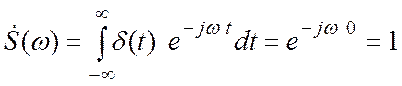           (3.22)

Во всем частотном диапазоне модуль спектра  – функции постоянен, фазовый спектр равен нулю.

Естественным является предположение о возможности представления (t) в виде обратного преобразования Фурье найденной спектральной функции