Сопротивление материалов: Учебно-практическое пособие, страница 22

10.4. Для двухопорной балки необходимо определить в начале реакции опор, а затем строить эпюры?

а) да;

б) нет;

в) это зависит от конструкции балки.

10.5 Знак изгибающего момента не зависит от внешних сил?

а) нет;

б) да;

в) при наличии сосредоточенного момента.

Литература

[2, стр. 22-90, 166-207, 208-247].

11.  Устойчивость сжатых стержней

11.1. Критические силы при сжатии стержня.

Стержень с прямолинейной осью теряет свою устойчивость по достижению величины силы сжатия, соответствующей критическому значению (F_кр). При упругом деформировании критическая сила Fкр определяется по формуле Эйлера:

                           F_кр = p²EJ_min/(m)²,  (H), 

гдеJ_min –минимальный осевой момент инерции поперечного сечения стержня относительно главных осей y или z (мм⁴).

E – модуль продольной упругости МПа;

  - длина стержня, мм

m - приведенная длина стержня, мм

m - коэффициент приведенной длины стержня (см. рис. 17 или справочник)

.

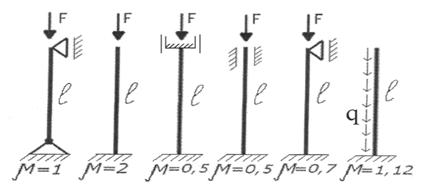
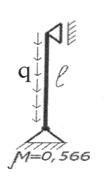
Рис.17. Значения коэффициента приведенной длины сжатого стержня m при различных способах его закрепления

 Таблица 6.

Конфигурация сечения		h>b
				табличные величины
Осевой момент инерции	Jz =bh3/12 Jy = hb3/12	Jz = Jy = pD4/64	Jz =Jy = pD4/64(1-c4)	Jz , Jy		Jz , Jy
Минимальный момент инерции	Jmin=Jy = hb3/12	Jz = Jy = Jmin	Jz = Jy =Jmin	Jy = Jmin		Jy = Jmin