Найпростіший щодо реалізації варіант визначається елементною базою. Так, лічильники на JK-тригерах з дубльованими входами потребують мінімуму додаткових елементів у міжрозрядних зв’язках (при викори- станні інверсного виходу і подвійних входів у старшому розряді схема на рис. 9.5,в не містить таких елементів) і можуть виявитися зручними для побудови на ІС жорсткої структури. На програмовних ІС економічнішими є схеми на D- і RSC-тригерах з динамічним керуванням. Крім того, для низки застосувань доцільною є побудова лічильників з довільним модулем і порядком лічби за схемами з послідовним і комбінованим переносом.
Проектування реверсивних лічильників. Особливості проектування розглянемо на прикладі побудовиреверсивного паралельного лічильника з модулем М = 5 і природним порядком лічби на JK-тригерах. Перемикальну таблицю доповнюємо стовпцем модифікації схеми (рис. 9.6,а): при m = 0 лічильник працює в режимі додавання, а при m = 1 – в режимі віднімання, а також стовпцем десяткового коду набору змінних i = =mQ2Q1Q0. В іншому методика проектування аналогічна.
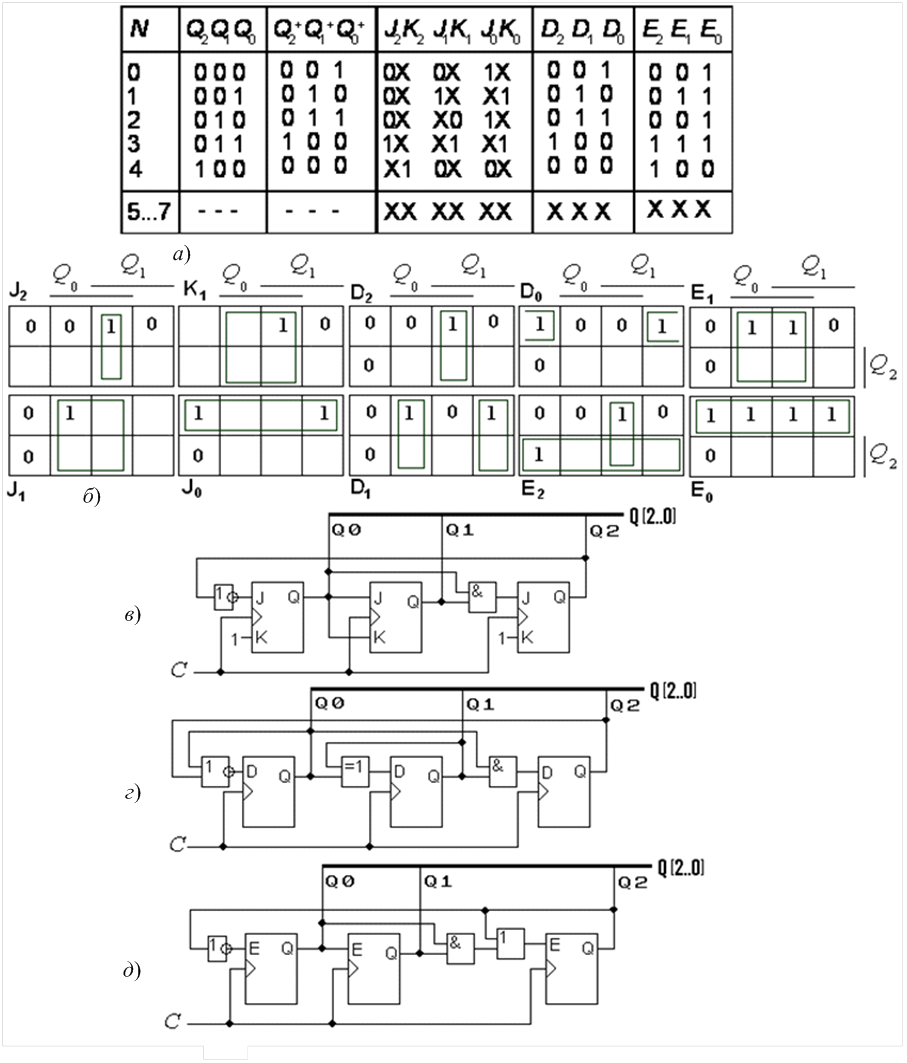
Рисунок 9.5
Безпосередньо з таблиці маємо К2 = К0 = 1, а інші функції збудження дістанемо з діаграм термів (на рис. 9.6,б порожнім клітинкам відповідають факультативні значення Х), застосовуючи прийоми їх сумісної мінімізації:
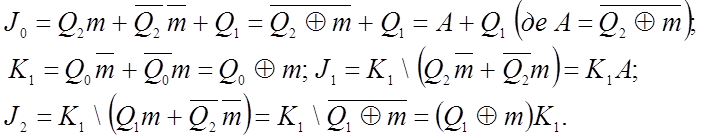
Цим рівнянням відповідає схема лічильника (рис. 9.6,в), напрямок лічби якого керується сигналом u/d = m(рис. 9.6,г).
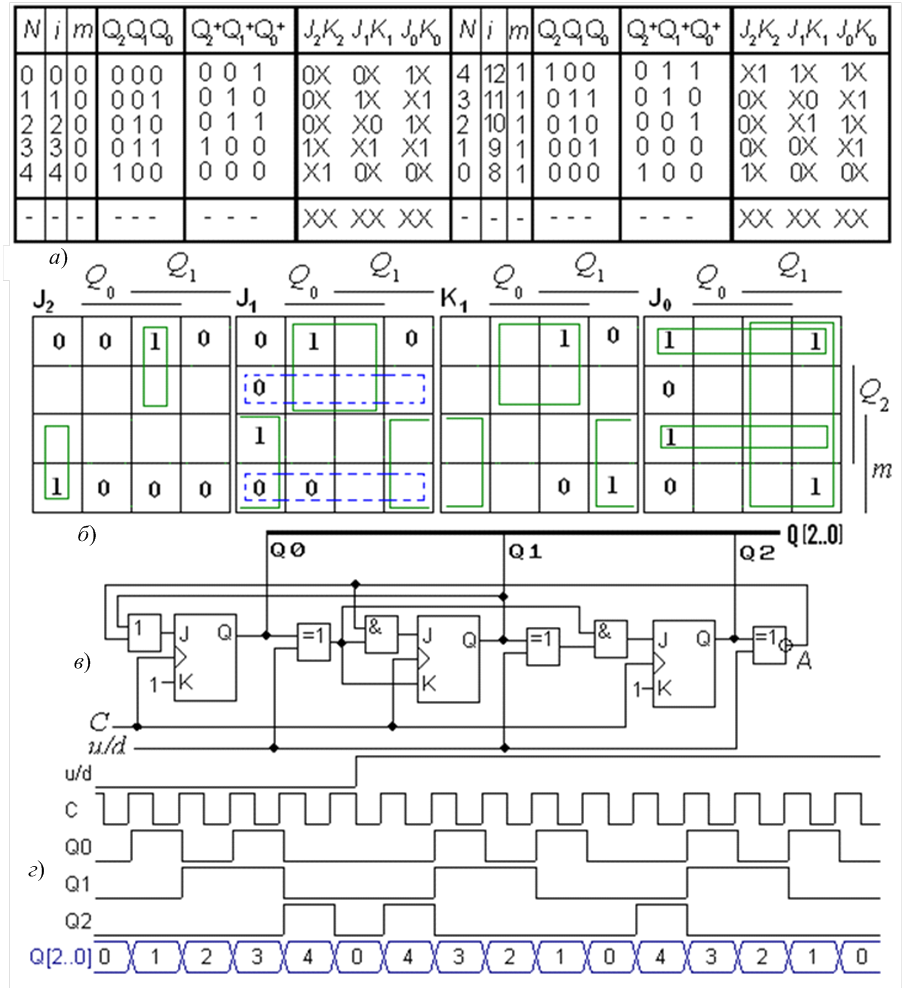
Рисунок 9.6
Подільники частоти
Загальна схема безвентильного подільника частоти. Будь-які лічильники можуть використовуватися як подільники частоти, коефіцієнт поділу якої на виході лічильника дорівнює його модулю лічби. Проте додаткові елементи (вентилі) у міжрозрядних зв’язках або потреба дубльованих входів у тригерів ускладнюють лічильники з довільним модулем і природним порядком лічби. З огляду на те, що в подільниках частоти порядок лічби не має значення, без його дотримання схему гранично спрощують.
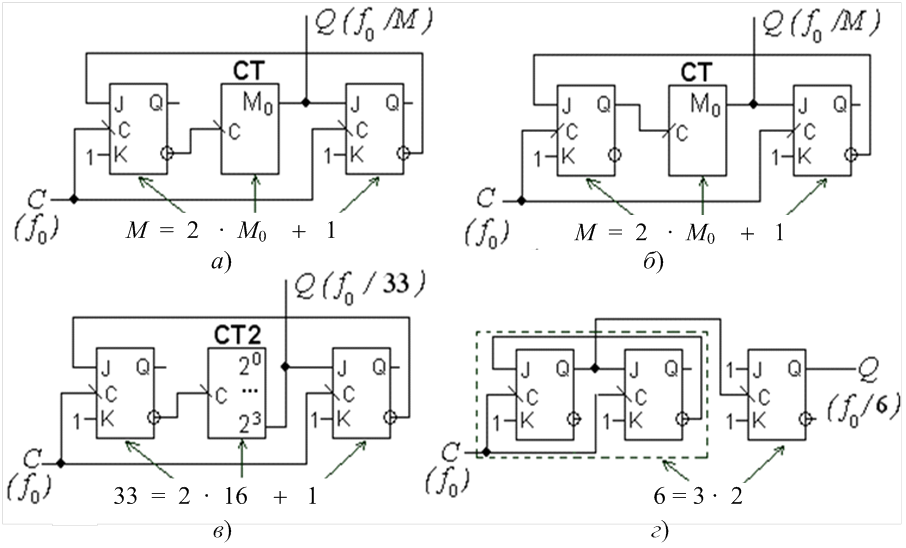
Рисунок 9.7
Безвентильні лічильники на JK-тригерах без дубльованих входів будуються шляхом збільшення модуля лічби на одиницю. Для цього лічильник з довільним модулем М0 охоплюють зворотним зв’язком за допомогою двох тригерів (варіанти схеми на тригерах з інверсним і прямим динамічним керуванням подано на рис. 9.7,а,б). При цьому перший тригер збільшує модуль вдвічі, а останній додає одиницю (через це для стислості його називають „одиничним”), тому в цілому модуль такого лічильника становить М = 2М0 + 1. Наприклад, охоплюючи таким зв’язком чотирирозрядний двійковий лічильник, дістанемо модуль М = 33 (рис. 9.7,в).
Так само утворюються лічильники з будь-яким непарним модулем, а при М0 = 1 дістанемо модуль М = 3 безпосереднім з’єднанням першого і одиничного тригерів (виокремлена частина на рис. 9.7,г). Для отримання парного модуля лічби досить послідовно ввімкнути лічильний тригер на вході або на виході. В останньому випадку (див. рис. 9.7,г) вихідні імпульси Q матимуть форму меандра.
Проектування. Побудову і аналіз функціонування безвентильного лічильника розглянемо на прикладі подільника частоти з модулем лічби (коефіцієнтом поділу) М = 11.
1. Розкладаємо модуль на числа степеня 2 та додаткові одиниці: М=11 = 10 + 1 = 2 ∙ 5 + 1 = 2 ∙ (4 + 1) + 1 = 2 ∙ (22 + 1) + 1. Підраховуємо потрібну кількість розрядів n= n2 + n1 як суму степенів два n2 та додаткових одиниць n1, яка в прикладі становить n= 3 + 2 = 5, тобто потрібно на один тригер більше мінімальної їх кількості за (4). Якщо є варіанти розкладу числа М, вибираємо такий, що потребує меншої кількості розрядів (наприклад, модуль М = 39 можна розкласти двома варіантами з розрядністю n= 7 та n= 8).
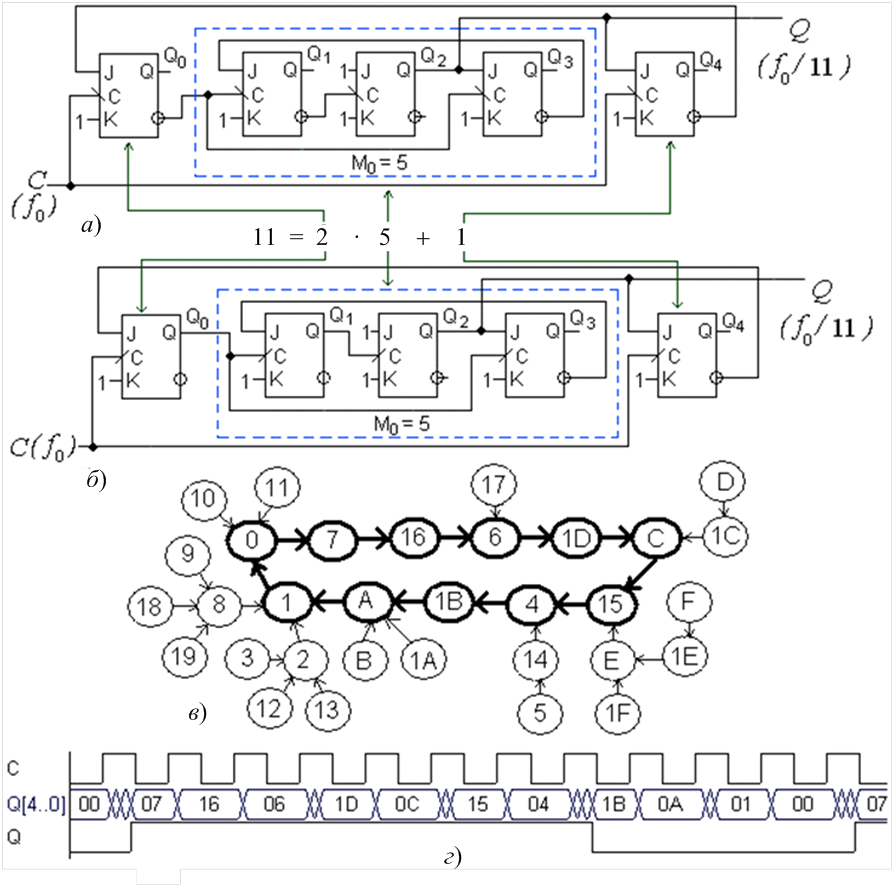
Рисунок 9.8
2. Поділяємо розкладання на блоки у вигляді (2 ∙ М0 + 1), наприклад, М= 11 = [2 ∙ (2 ∙ 2 + 1) + 1] та реалізуємо ці блоки за типовою схемою (див. рис. 7,а,б) з використанням лічильних тригерів або лічильників для степенів числа 2 і одиничних тригерів для одиниць (рис. 9.8,а,б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.