Информатика и выч. техника \ Проектирование цифровых устройств

Проектування цифрових пристроїв на основі САПР QUARTUS II: Практикум, страница 38

Мета роботи: дослідження типових арифметичних пристроїв – суматорів, арифметико-логічних пристроїв, помножувачів, подільників і компараторів; побудова ЦКП на суматорах і компараторах; засвоєння основ створення ієрархічного проекту на рівні блок-схеми.

ДОМАШНЄ ЗАВДАННЯ

! Спроектувати заданий згідно з варіантом (див. додатки) пороговий елемент на суматорах і компараторах.

СТИСЛІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Арифметичні пристрої: двійкові суматори, комбінаційні помножувачі, арифметико-логічні пристрої, цифрові компаратори розглянуто в [2]. Основні з них подані в табл. 6.1, 6.2.

Застосування арифметичних пристроїв для побудови ЦКП

Арифметичні пристроїможуть використовуватись не тільки для виконання арифметичних операцій, але й для побудови пристроїв, пов’язаних із порівнянням кодів, визначенням кількості вхідних сигналів, що набувають значення логічної  1 тощо. До таких ЦП належать, зокрема, порогові елементи – ЦКП, на виході яких встановлюється рівень логічної  1, якщо не менш, ніж на k із довільної кількості m входів сигнали набувають рівня логічної  1. Окремим випадком порогових пристроїв є мажоритарний елемент – ЦКП, на виході якого виникає рівень логічної  1, якщо на більшості з його непарної кількості m входів діють рівні логічної  1.

Приклад. Для прикладу розглянемо принцип побудови мажоритарного елемента на m = 7 входів, тобто пристрою з порогом k = 4. Потрібна для цього кількість елементів І-НЕ різко зростає зі збільшенням m і стає неприйнятною. Ідея використання суматорів полягає в тому, що спочатку підраховуємо кількість логічних одиниць на входах, а потім встановлюємо, чи не перевищує вона потрібний поріг k.

Нагадаємо попередньо, що індекси i на вхідному і вихідному  полях умовного графічного позначення суматора (див. рис. 6.1,а) вказують на вагу його розрядів 2i. З огляду на це підраховуємо кількість одиниць на входах х1...х7 за допомогою двох однорозрядних та одного дворозрядного суматорів (рис. 6.1,а), виконуючи  з’єднання з урахуванням ваги розрядів. Підсумок зчитуємо з виходів останнього суматора як S = с222 + s121 + s020, тобто у вигляді двійкового числа с2s1s0. Перенесення ум = с2 і є виходом мажоритарного  елемента “4 з 7", бо S ≥ 4 при с2 = 1.

Аналогічно проектуємо й пороговий елемент, наприклад, при m = 7, k = 5. Згідно з таблицею (рис. 6.1,б) мінімізуємо його функцію (рис. 6.1,в)       yп = (s0 + s1) с2 та реалізуємо її на основі тієї ж схеми (див. рис. 6.1,а). Отже, на виході yм встановлюється рівень логічної  1 за виникнення одиниць не менш ніж на 4 входах, а на виході уп – не менш ніж на 5 входах із 7.

а)

б)

в)

Рисунок 6.1

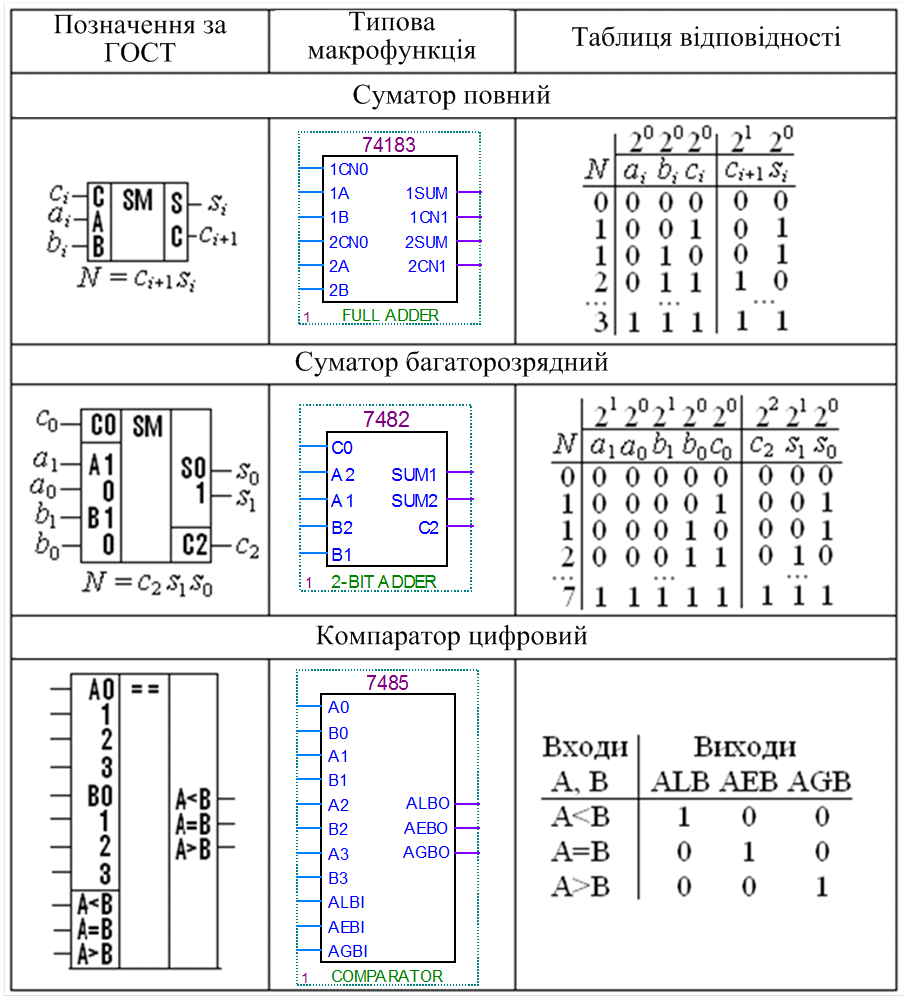
Таблиця 6.1 – Макрофункції арифметичних пристроїв


Таблиця 6.2 – Мегафункції арифметичних пристроїв

Символ

Основні параметри

lpm_add_sub (Adder/Subtractor):

LPM_WIDTH – розрядність вхідних і вихідної шин;

LPM_REPRESENTATION –  зобра­ження даних: зі знаком ("SIGNED"), без знаку ("UNSIGNED");

LPM_DIRECTION – тип операції: додавання ("ADD"), віднімання ("SUB");

сin (Carry-in), cout (Carry-out) –  вхі­дний і вихідний переноси.

lpm_compare (Comparator):

LPM_WIDTH – розрядність вхідних шин dataa[] = А та datab[] = В.

Входи        Функція

А < B         alb    

А = B         aeb            

А > B         agb

А ³ B         ageb

А ¹ B         aneb

А £ B           aleb

lpm_mult (Multiplier):

LPM_WIDTHA – розрядність множеного dataa[];

LPM_WIDTHB – розрядність множника datab[];

LPM_WIDTHP = LPM_WIDTHA +  + LPM_WIDTHB – розрядність добутку result[].

lpm_divide (Divider):

LPM_WIDTHN – розрядність діленого numer[] і частки quotient[];

LPM_WIDTHD – розрядність дільника denom[] і залишку remain[].

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Як слід каскадувати з метою збільшення розрядності: 1) суматори, 2) АЛП, 3) компаратори?

Скачать файл