Для наочності будуємо робочий цикл перемикального графу ГКП. Під час зсуву числа з послідовності символів на один крок у бік старших розрядів значення початкового коду N = Q2Q1Q0 подвоюється (наприклад, 001 ® 010) і до молодшого розряду додається ще наступний символ xN послідовності, тобто з надходженням чергового синхроімпульсу матимемо код N+ = 2N + xN. Але якщо є одиниця в старшому розряді, у наступному такті зсуву вона зникає, тому її вагу 2n-1 перед подвоєнням треба відняти. Отже, наступний код можна визначити з виразу:
N+ = 2N + xN, якщо N < 2n-1; N+ = 2(N – 2n-1 ) + xN, якщо N ³ 2n-1. (8.1)
Так, у прикладі при n = 3 перший код утворюється трьома нулями послідовності символів (000111), тобто N = Q2Q1Q0 = 0. Другий код N+=2×0+1=1, бо N < 4 і наступний символ послідовності xN = 1; так само третій код становить N+ = 2×1 + 1 = 3 і т.д. Після останнього символа з періоду послідовності переходимо до його початку. У підсумку визначаємо робочий цикл N = Q2Q1Q0 = (000111) = 0, 1, 3, 7, 6, 4, який відображаємо перемикальним графом (рис. 8.1,а).
FПримітка. Робочий цикл можна визначити і безпосередньо з послідовності символів 000111000111... просуванням по ній трьох розрядів, але це не зручно для великих модулів і, як буде видно з подальшого, для побудови повного графу.
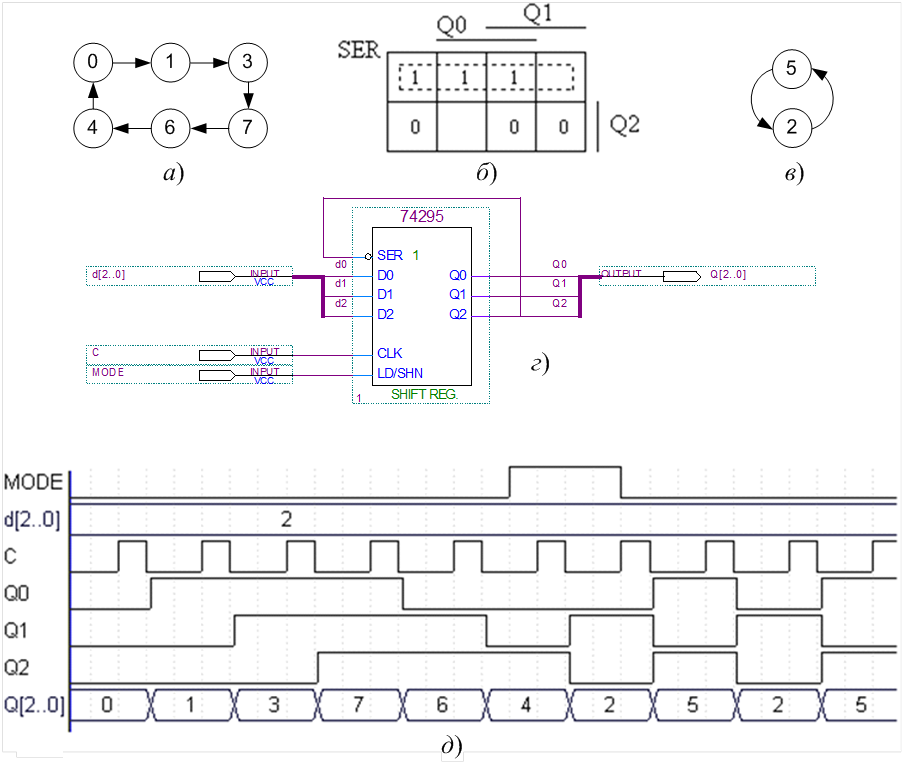
Рисунок 8.1 – Проектування ГКП
2. Мінімізуємо функцію збудження за входом послідовного введення SER, який для регістра прямого зсуву є входом молодшого розряду, отже, для регістра на D-тригерах функція має вигляд SER = Q0+ . Тому діаграму термів (Вайча-Карно) можна побудувати і без таблиці відповідності (за багатьох розрядів така таблиця стає неозорою). Виходимо з того, що парні коди N = Q2Q1Q0 закінчуються на 0, а непарні – на 1, тому в клітинку діаграми з номером N вписуємо значення Q0+ = 0, якщо наступний код робочого циклу є парний, і Q0+ = 1, якщо непарний. Так, на діаграмі рис. 8.1,б номери клітинок відповідають станам N = Q2Q1Q0, що є вершинами робочого циклу графу, тому до нульової клітинки N = 0 вписуємо 1, бо наступний код N+ = 1 є непарний; переходимо до вершини N = 1 і вписуємо до клітинки з цим номером також одиницю, бо наступний код N+ = 3 теж є непарний і т. д. У підсумку заповнюємо шість клітинок відповідно до робочого циклу, а в двох порожніх клітинках функція має факультативні значення, бо у станах, що їм відповідають, за нормальної роботи пристрій не перебуває. Мінімізуючи звичайним чином, отримуємо функцію збудження
![]() .
(8.2)
.
(8.2)
3. Перевіряємо функціонування пристрою, якщо випадково (внаслідок збою, дії завади або після ввімкнення джерела живлення) він опиниться в хибному стані поза межами робочого циклу. Пристрій, що автоматично за кілька тактів повертається до робочого циклу, є самовідновний, інакше – несамовідновний. З метою перевірки на самовідновність будуємо повний перемикальний граф. Для цього беремо будь-який стан поза робочим циклом і за (1) визначаємо наступний стан, але значення xN підставляємо тепер з діаграми термів: для тих кодів, які згідно з виконаною мінімізацією входять до об’єднань одиниць, xN = 1, а для всіх інших xN = 0. Так, зі стану N=2 з надходженням синхроімпульсу ГКП перейде до стану N+=2×2+1=5, бо N< 4 і xN = 1, а зі стану N = 5 повернеться до N+=2(5–4)+0=2, тобто замкнеться хибний цикл (рис. 1,в) з модулем 2, отже, ГКП є несамовідновний.
Такий ГКП, реалізований згідно з (2) на регістрі зсуву з перехресним зворотним зв’язком та інвертуванням біта старшого розряду, який називається також лічильником Джонсона (рис. 8.1,г), функціонує за часовими діаграмами на рис. 1,д. З метою випробування регістр керується сигналом MODE = LD/SHN (завантаження/зсув): при MODE = 0 він функціонує як регістр зсуву, а при MODE = 1 з надходженням синхроімпульсу до нього завантажується в паралельному коді слово зі входів d[2..0], яке імітує збій з переходом до хибного стану. З діаграм видно, що в кожному розряді відповідно до тактів синхроімпульсів за нормальної роботи пристрою просувається послідовність символів по три нулі і три одиниці поспіль (отже, безпосередньо з діаграми легко записати період послідовності символів). Зі зсувом у розрядах ці послідовності утворюють вихідні коди згідно з робочим циклом графу, але після збою послідовність порушується і пристрій не в змозі самостійно вийти з хибного циклу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.