Проектування цифрових пристроїв на основі САПР QUARTUS II: Практикум, страница 22

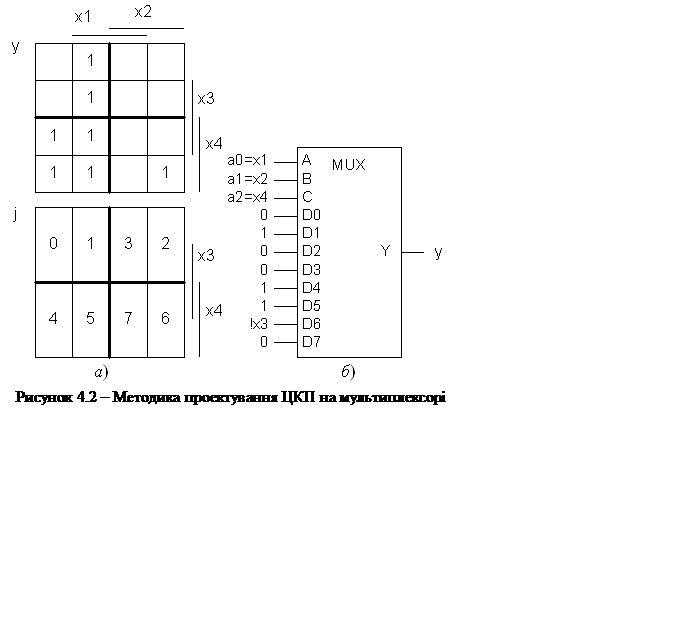
2. Вибираємо мультиплексор з кількістю адресних входів k на одиницю менше кількості змінних (у прикладі k=m–1=3, тобто мультиплексор 8:1). До адресних входів приєднуємо змін­ні, від яких функція залежить більшою мірою, тобто формуємо адресний код j (у прикладі j=a₂a₁a₀ = = x₄x₂x₁) і розбиваємо діаграму функції y на 2^k піддіаграм. Для цього у кожну клітинку діаграми j (на рис. 4.2,а нижня діаграма) вписуємо десятковий код j= x₄x₂x₁ відповідно до рисок цих змінних, не звертаючи уваги на аргумент x₂, що не входить до адреси. Отже, діаграма виявляється розбитою на 8 піддіаграм (з двох клітинок кожна), які і визначають номери j інформаційних входів мультиплексора, що з'єднуються з виходом y.

3. Визначаємо сигнали d_j(х₃) на входах мультиплексора як функції вільної змінної, не приєднаної до адресних входів. Для цього зміст клітинок часткових діаграм з номерами j зчитуємо з діаграми у: d₀=d₂=d₃=d₇= 0, d₁=d₄=d₅=1, d₆=.

4. Згідно з функціями d_j будуємо ЦКП (рис. 4.2,б). Легко переконатися, що пристрій функціонує відповідно до діаграми термів. Наприклад, коли х₄х₂х₁ = 0101, тобто і = 5 маємо у₂ = d₅ =1. Отже, схема виявляється вдвічі простішою відносно рис. 4.1,б – потрібен лише один додатковий інвертор на вході d₆.

5. Аналогічно проектуємо ЦКП на мультиплексорі 4:1 меншої розрядності – з двома адресними і чотирма інформаційними входами. До адресних входів приєднуємо дві змінні, від яких функція залежить більшою мірою (у прикладі один з трьох рівноцінних за цим критерієм варіантів), тобто формуємо адресний код j = a₁a₀ = x₂x₁ і розбиваємо діаграму функції y на чотири піддіаграми (рис. 4.3,а). Розглядаючи кожну з піддіаграм як діаграму термів функції двох змінних d_j(x₃, x₄) і мінімізуючи звичайним чином, визначаємо сигнали: d₁ = 1, d₃ = 0, d₀ = х₄, d₂ =. Шляхом порівняння з іншими двома варіантами адресного коду вибираємо перший (рис. 4.3,б) і, порівнюючи його з ЦПП на рис. 4.2,б, вважаємо кращим, бо він потребує простішого мультиплексора без надмірного ускладнення кіл для формування вхідних сигналів (потрібно по одному елементу НЕ та І).

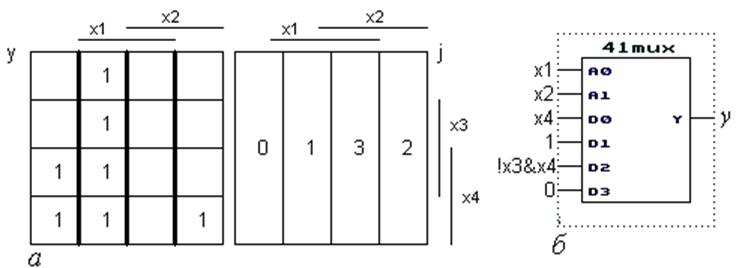
Рисунок 4.3 – Проектування ЦКП на мультиплексорі 4:1

І, нарешті, так само проектуємо ЦКП на мультиплексорі 2:1 (рис. 4.4,а), вибираючи варіант адресного входу j=a= x₁:  (рис. 4.4,б). З порівняння можна дійти висновку, що остання реалізація ЦКП потребує менше ресурсу ІС, ніж попередні.

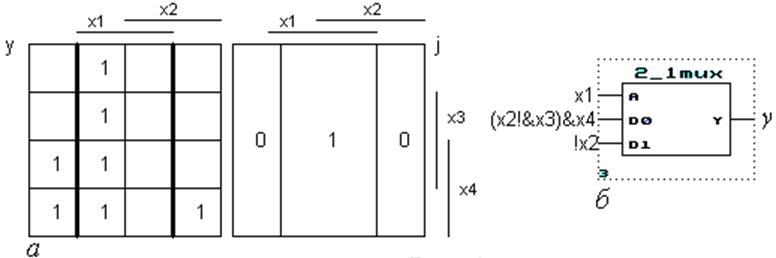
Рисунок 4.4 – Проектування ЦКП на мультиплексорі 2:1

Слід відзначити, що якщо в логічному виразі функції можна винести за дужки спільний аргумент х_i, то ЦКП спрощується наданням стробовому входові значення G = х_i при використанні мультиплексора-селектора зі звичайним (без третього стану) виходом. Крім того, якщо логічні функції на окремих інформаційних входах мультиплексора виявляються досить складними, то їх у свою чергу також можна реалізувати на мультиплексорах. Побудова ЦКП з кількома виходами зводиться до проектування кількох пристроїв для кожної функції окремо. Якщо з цією метою скористатися ІС мультиплексорів зі спільними адресними входами, цим входам доцільно надати ті змінні, які найбільшу кількість разів входять до обох функцій.

Таблиця 4.1 – Мегафункції логічних елементів