После выбора структурной схемы проектируемой системы и отображения в окне-списке моделей её элементов надо сообщить средству SISOTOOL, какие из этих моделей будут использованы в качестве моделей объекта управления (G) и датчика (H). По умолчанию все элементы структурной схемы системы являются пропорциональными звеньями с коэффициентами, равными единице, о чём свидетельствуют единичные цифры в текстовых окнах G=, H=, F=, C=, расположенных в нижней части поля SystemData (рис. 6).
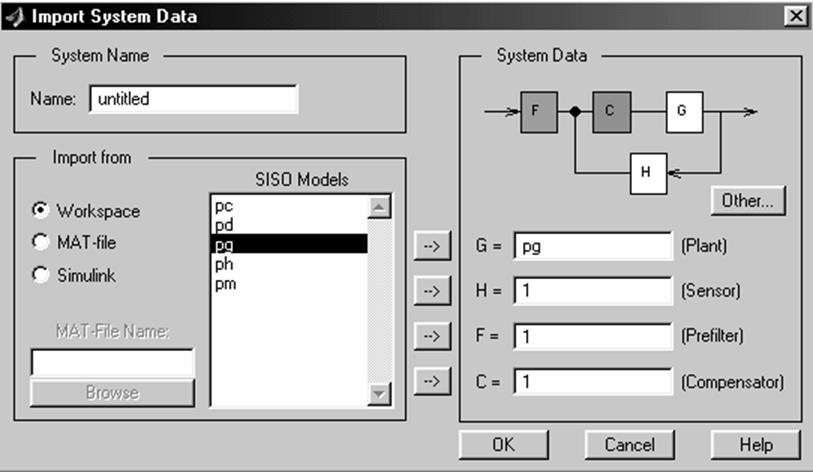
Рис. 6
3.3. Чтобы импортировать модели элементов неизменяемой части из окна-списка SISOModels в средство SISOTOOL:
а) выберите желаемую модель в окне-списке SISOModels (рис. 6),
например модель с названием pg, c целью её использования в качестве модели одного из блоков G,H, например блока G;
б) щёлкните кнопку со стрелкой, указывающей на название блока проектируемой системы, модель которого вы хотите установить. В данном случае щёлкните кнопку со стрелкой, указывающей на название блока управления G =. В текстовом окне, соответствующем блоку, модель которого вы устанавливаете, появляется название модели, выбранной вами в окне-списке SISOModels, в данном случае в текстовом окне G= появляется название модели pg;
в) нажмите кнопку OK. Как уже ранее упоминалось (см. c. 5,6), вы можете создать все или часть моделей элементов неизменяемой части проектируемой системы в текстовых окнах поля SystemData .
3.4. Чтобы создать модели элементов неизменяемой части проектируемой системы в текстовых окнах поля SystemData диалогового окна ImportSystemData (рис. 7):
введите в текстовые окна с названием G=, H= команды типа tf,zpk,ss, соответствующие заданным математическим моделям объекта управления и датчика.
Пример. Пусть математическая модель объекта управления представлена передаточной функцией W(p)=11.5/[p(p+2)(p+6)]. Тогда для создания MATLAB’обовской модели этого объекта введите (рис. 7) в текстовое поле с названием G= команду
tf(11.5,[1 8 12 0]).
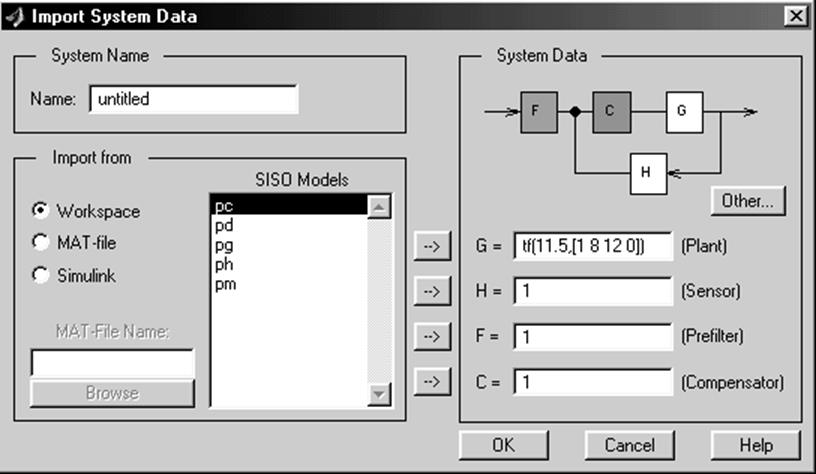
Рис. 7
После того как вы выбрали структурную схему и установили модели всех элементов неизменяемой части проектируемой системы, можете дать название этой системе.
3.5. Чтобы дать название проектируемой системе:
а) щёлкните в текстовом окне Name(название), расположенном в верхней части поля System Nameдиалогового окна ImportSystemData (рис. 7);
б) введите в текстовое поле Name название, выбранное вами для проектируемой системы, например введите sys_d;
в) щёлкните кнопку OK.
В результате установки моделей неизменяемой части проектируемой системы и её названия в окне средства SISOTOOL(рис. 8) появляются изображения корневого годографа и логарифмических частотных характеристик разомкнутой нескорректированной системы, другими словами, системы, передаточная функция которой равна произведению передаточных функций объекта управления и датчика. При этом в заголовке этого окна отображается выбранное вами название проектируемой системы.
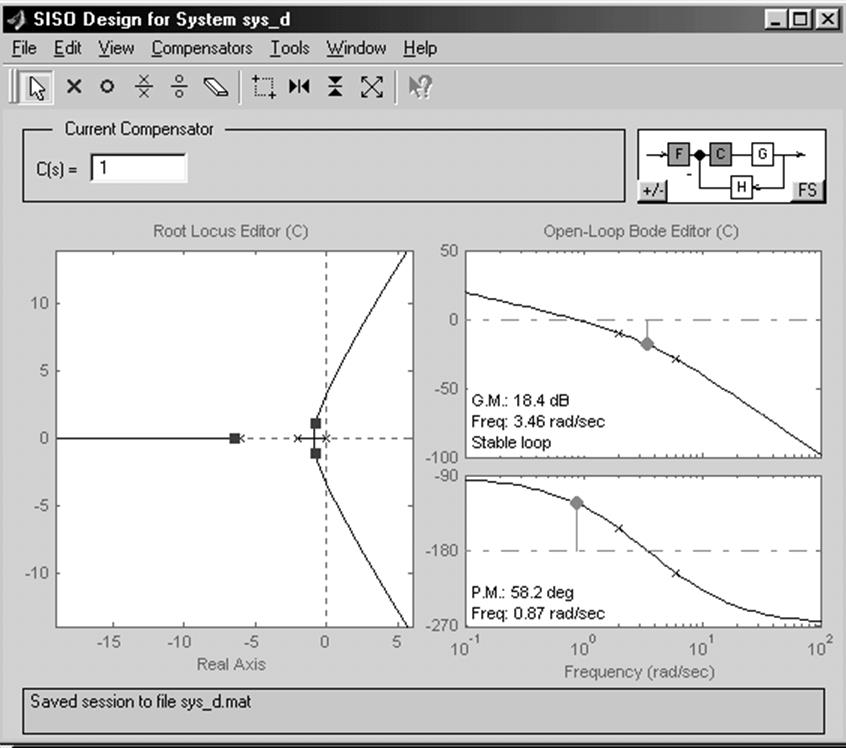
Рис. 8
Кстати, по умолчанию корневой годограф и логарифмические частотные характеристики разомкнутой системы окрашены в синий цвет. Полюсы/нули неизменяемой части проектируемой системы, регулятора и предварительного фильтра изображаются в виде крестиков и ноликов, причем цвет полюсов/нулей неизменяемой части проектируемой системы - синий(blue), цвет полюсов/нулей регулятора - красный(red), цвет полюсов/нулей предварительного фильтра - зеленый (green). Следует упомянуть, что вид и цвет полюсов замкнутой системы – квадратик(square) и красный.
На логарифмических частотных характеристиках
разомкнутой системы полюсам/нулям неизменяемой части проектируемой системы и
регулятора соответствуют маркеры в виде крестиков и ноликов, цвет которых
совпадает с цветом этих полюсов/нулей. Ординаты маркеров для вещественных
полюсов/ нулей равны их модулям (абсолютным значениям). Например, если полюс
или нуль равен –5,2, то ордината соответствующего маркера (крестика или нолика)
равна 5,2. Ордината маркера для комплексно-сопряженных полюсов/нулей
определяется значением квадратного корня из суммы квадратов вещественной и
мнимой частей, т.е. значением модуля этих полюсов/нулей. Например, если
комплексно-сопряженные полюсы или нули равны –5,2±j8, то ордината соответствующего маркера (крестика или
нолика) равна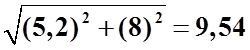 
.
В передаточной функции разомкнутой системы ее
вещественным полюсам/нулям 
соответствует сомножитель типа двучлена 
, где 
- постоянная времени, 
. В передаточной функции разомкнутой системы ее
комплексно-сопряженным полюсам/нулям 
,
соответствует сомножитель типа трехчлена
.
Здесь 
- постоянная времени
(TimeConstant), 
- относительный
коэффициент затухания (Damping), 
-модуль. Асимптотические логарифмические амплитудно-частотные
характеристики таких сомножителей состоят из отрезков двух прямых [3,4],
которые сопрягаются при частоте 
для двучленов 
и при частоте 
для трехчленов 
. Следовательно, ординаты маркеров
(крестиков и ноликов) на логарифмических частотных характеристиках,
отображаемых в графических окнах средства SISOTOOL,
можно рассматривать как сопрягающие частоты сомножителей передаточной функции,
причем нолик соответствует сомножителю, расположенному в числителе, а крестик - сомножителю, расположенному в знаменателе этой передаточной функции.
В
средстве SISOTOOL сопрягающие частоты 
и 
называют
собственными частотами (NaturalFrequency)
сомножителей передаточной функции или собственными частотами ее нулей/полюсов.
В этом средстве также для вещественных нулей/полюсов принято считать
относительный коэффициент затухания (Damping)
равным 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.