10.4.3.
Чтобы получить сведения о передаточной функции элемента неизменяемой части
системы, включая приведённый коэффициент усиления, нажмите на
кнопку ShowTransferFunction, расположенную в области этого элемента в окне на
рис. 37, например, на кнопку, расположенную в области PlantModel: W1.
Появляется окно, в данном случае - окно W1
(рис. 37), содержащее передаточную
функцию данного элемента в форме zpk (zero/pole/gain), другими
словами, в приведенной форме. В данном случае приведенный коэффициент усиления
объекта управления равен 48,7485, а истинный коэффициент усиления ![]() =48,7485/(5.988
=48,7485/(5.988![]() 1.988)= =4,095. Заметим, что информация о передаточных
функциях элементов неизменяемой части системы дается в приведенной форме независимо
от того, в каком виде вы импортировали в средство SISOTOOL эти
функции. Данное обстоятельство несколько усложняет определение истинного
коэффициента нескорректированной системы.
1.988)= =4,095. Заметим, что информация о передаточных
функциях элементов неизменяемой части системы дается в приведенной форме независимо
от того, в каком виде вы импортировали в средство SISOTOOL эти
функции. Данное обстоятельство несколько усложняет определение истинного
коэффициента нескорректированной системы.
Окно SystemData позволяет изменить название неизменяемой части.
10.4.4. Чтобы изменить название неизменяемой части проектируемой системы:
а) введите новое название в текстовое окно с названием SystemName(название проектируемой системы);
б) нажмите кнопку OK.
Замечание. Новое название, которые вы дали неизменяемой части проектируемой системы, будет использовано только тогда, когда вы захотите вновь создать регулятор, соответствующий структурной схеме новой проектируемой системы.
10.5. Информация о передаточной функции (нулях и полюсах) регулятора
В поле CurrentCompensator для передаточной функции регулятораC(s) высвечивается то или иное выражение в зависимости от выбранного вами формата (вида) представления передаточной функции регулятора. Желаемый формат этой передаточной функции можно установить, используя команду Format меню Compensators окна SISODesignTool, после выполнения которой появляется диалоговое окно SISOToolPreferences(настройка свойств средства SISOTOOL), открытое на вкладке Options (рис. 38).
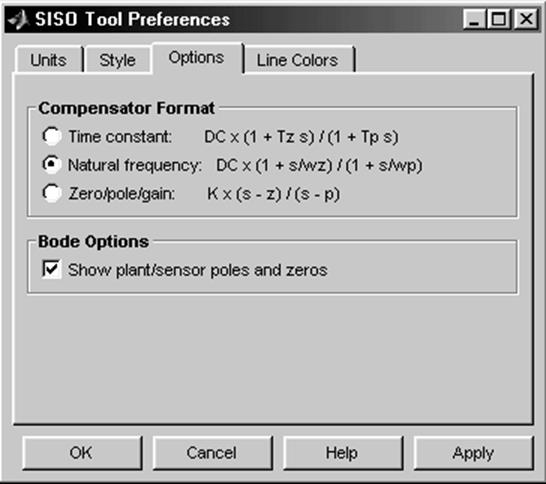
·
в стандартной форме (формат типа TimeConstant), т.е. в
виде произведения сомножителей типа ![]() и
и ![]() , расположенных в числителе и
знаменателе передаточной функции. При этом в окне C(p)= высвечивается истинный коэффициент регулятора (DC);
, расположенных в числителе и
знаменателе передаточной функции. При этом в окне C(p)= высвечивается истинный коэффициент регулятора (DC);
·
в форме с собственными частотами ![]() (формат
типаNaturalFrequency), т.е. в виде произведения сомножителей типа
(формат
типаNaturalFrequency), т.е. в виде произведения сомножителей типа ![]() и
и ![]() ,
расположенных в числителе и знаменателе передаточной функции. При этом в окне C(p)= также высвечивается истинный коэффициент усиления
регулятора (DC);
,
расположенных в числителе и знаменателе передаточной функции. При этом в окне C(p)= также высвечивается истинный коэффициент усиления
регулятора (DC);
·
в приведенной форме (формат типа Zero/Pole/Gain), другими
словами, в форме нулей, полюсов,
приведенного коэффициента усиления, т.е.
в виде произведения сомножителей типа ![]() и
и 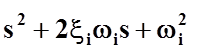 , расположенных в числителе и знаменателе передаточной
функции. При этом в окне C(p)=
высвечивается приведенный коэффициент усиления регулятора (K).
, расположенных в числителе и знаменателе передаточной
функции. При этом в окне C(p)=
высвечивается приведенный коэффициент усиления регулятора (K).
В качестве примера на рис. 39 для одного и того же регулятора приведены выражения его передаточной функции в стандартной форме - а, в форме с собственными частотами - б и в приведенной форме - в.

а

б

в
Рис. 39
В данном случае истинный и приведенный коэффициенты усиления соответственно равны 9,73 и 5,3.
Рекомендация. При проектировании регулятора с использованием комбинации методов корневого годографа и логарифмических частотных характеристик удобно придерживаться формата типа NaturalFrequency.
 Если выражение для передаточной функции не умещается в
полеCurrentCompensator,
то в этом поле появляется выражение вида рис. 40. Чтобы в этом случае
получить информацию о
Если выражение для передаточной функции не умещается в
полеCurrentCompensator,
то в этом поле появляется выражение вида рис. 40. Чтобы в этом случае
получить информацию о
рис. 40 передаточной функции в явном виде, попытайтесь
растянуть окно SISO Design Tool.
Надо отметить, что диалоговое окно SISOToolPreferencesможно вызвать другим путем, выполняя одноименную команду из меню Edit или используя команду ToolboxPreferences из меню File и открывая вкладку SISOTool.
11. СИНТЕЗ ПРЕДВАРИТЕЛЬНОГО ФИЛЬТРА
Закон управления с прямой и обратной связью (рис. 4.5), другими словами, использование наряду с регулятором предварительного фильтра позволяет в достаточной степени автономно решать две основные задачи, возникающие при построении систем управления. Первая из этих задач, по существу задача регулирования, заключается в том, чтобы уменьшить влияние на работу системы возмущений, к которым относятся возмущающие воздействия, шум измерения управляемой величины, неопределенность и изменчивость математической модели объекта управления. Второй из упомянутых задач является задача слежения, другими словами, задача воспроизведения с заданной точностью задающего воздействия.
Если предполагается применить предварительный фильтр, то вторая задача решается в процессе синтеза регулятора в отсутствие задающего воздействия и сводится к поискам такого закона управления по ошибке, который обеспечивает желаемое расположение полюсов замкнутой системы. При решении данной задачи можно не обращать особого внимания на требования, предъявляемые к воспроизведению задающего воздействия. Например, можно выбрать коэффициент усиления разомкнутой системы (разомкнутого контура) и порядок астатизма ниже требуемых значений, обусловленных заданной точностью воспроизведения задающего воздействия. Тем самым при синтезе регулятора можно ослабить ограничения на вид логарифмической амплитудно-частотной характеристики разомкнутой системы (разомкнутого контура) в области низких частот. Также не следует особенно стремиться лишь за счет регулятора обязательно выполнить требования, касающиеся значения перерегулирования при сигнале, приложенном к входу замкнутого контура, расположенного за предварительным фильтром (рис.4,5). Разумеется, что на эти издержки можно согласиться в двух случаях: а) если возникают трудности с синтезом регулятора, который бы обеспечил достаточные запасы устойчивости при заданном коэффициенте усиления разомкнутой системы (разомкнутого контура) и требуемом числе интеграторов; б) или наоборот, если за счет регулятора удалось добиться достаточных запасов устойчивости, следовательно, небольшой колебательности системы, но при этом не удается обеспечить прохождение логарифмической амплитудно-частотной характеристики разомкнутой системы (разомкнутого контура) выше границы точности (рис. 26).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.