Проектирование линейных систем управления с SISO DESIGN TOOL / MATLAB: Учебное пособие, страница 11

. 

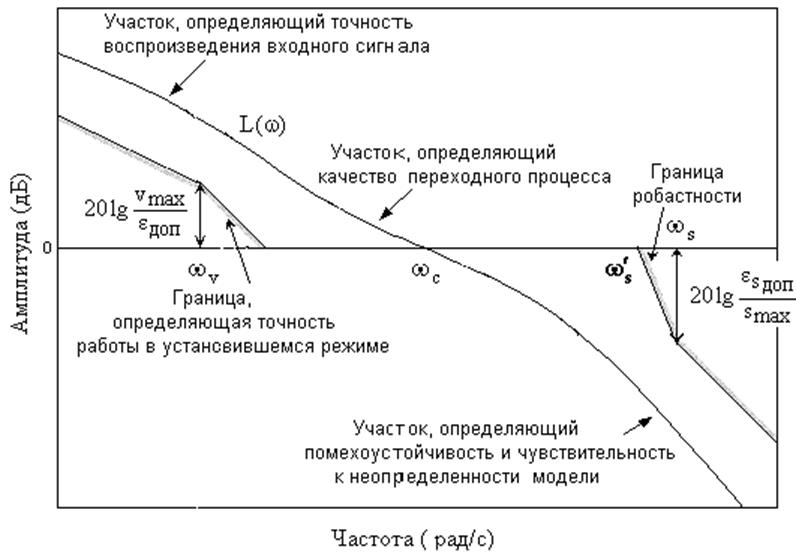
Рис. 26

Отсюда нетрудно найти уравнение нижней предельной границы точности работы системы в установившемся режиме

 .

          Наряду с  заданной точностью воспроизведения гармонического воздействия проектируемая система должна, как правило, безошибочно воспроизводить в установившемся режиме постоянное задающее воздействие, т.е. должна обладать астатическими  свойствами. Следовательно, низкочастотный участок логарифмической амплитудно-частотной характеристики проектируемой разомкнутой системы  должен иметь наклон, по меньшей мере равный –20 дБ/дек. Если  желаемый порядок астатизма равен единице, то граница точности работы в установившемся режиме в диапазоне частот гармонического задающего воздействия обязана иметь вид  луча (рис. 26), выходящего из точки с координатами , и имеющего наклон –20 дБ/дек. Разумеется, проектируемая замкнутая система будет обеспечивать требуемую точность воспроизведения задающего воздействия, когда логарифмическая амплитудно-частотная характеристика разомкнутой системы в диапазоне частот  будет располагаться не ниже такой границы точности.

          Вторая граница желаемого расположения логарифмической амплитудно-частотной характеристики разомкнутой системы (граница робастности) формируется в соответствии с требованиями помехоустойчивости. Это требование обусловлено наличием высокочастотного шума датчика (шума измерений), возникающего в процессе измерения управляемой величины (рис. 19). Пусть шум датчика занимает спектр частот, лежащий выше нижней предельной частоты , заметно превышающей верхнюю предельную частоту  спектра задающего воздействия. Предположим, что известны максимальное значение каждой гармонической составляющей   шума измерения и допустимая величина установившейся ошибки  по шуму измерения. Тогда условие малого влияния шума измерения на управляемую величину в установившемся режиме можно записать применительно к логарифмической амплитудно-частотной характеристике разомкнутой системы в виде

.

Данное соотношение получено с учетом того, что при малых значениях амплитудно-частотной характеристики разомкнутой системы  амплитудно-частотная характеристика замкнутой системы принимает значения, почти не отличающиеся от значений первой из упомянутых характеристик.

          Итак, верхняя предельно допустимая граница робастности, называемая также границей помехоустойчивости, определяется выражением

.

Для того чтобы проектируемая система подавляла в достаточной степени шум измерения, ее логарифмическая амплитудно-частотная характеристика должна проходить не ниже границы помехоустойчивости  на частотах шума измерения.           

    Заметим, чем меньшие значения принимает логарифмическая амплитудно-частотная характеристика проектируемой системы в области высоких частот, тем меньшее влияние на  управляемую величину оказывает неопределенность модели объекта управления в этой области и тем выше робастность (грубость) системы. Отсюда второе название границы - граница робастности. Если проблема робастности превалирует над задачей помехоустойчивости, то граница робастности строится исходя из несколько преобразованного критерия робастной устойчивости системы [4]:

,

где   логарифмическая  частотная   характеристика

отражает отношение номинальной амплитудно-частотной характеристики объекта управления к аддитивной неопределенности  в области высоких частот. В этом случае граница робастности определяется как . Здесь частота  является частотой, при которой логарифмическая  частотная   характеристика пересекает ось частот.

Пример. Пусть возмущенная передаточная функция объекта управления, учитывающая неопределенность динамики объекта на высоких частотах, имеет вид

,

где - номинальная передаточная функция объекта управления.

При этом передаточная функция аддитивной неопределенности определяется выражением

.

Отсюда асимптотическая логарифмическая частотная характеристика, определяемая  как   и  построенная    по отношению передаточных  функций , имеет вид, представленный на рис. 27.

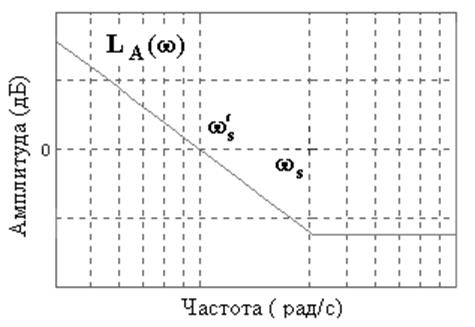
Рис. 27

          Следует сказать, что  хорошая замкнутая система управления должна иметь достаточно широкую полосу пропускания и малую колебательность. Полоса пропускания замкнутой системы управления зависит от частоты среза , при которой логарифмическая амплитудно-частотная характеристика разомкнутой системы пересекает ось частот на уровне 0 дБ (рис. 26). Установлено, что для обеспечения малой колебательности (малого перерегулирования) наклон среднечастотного участка логарифмической амплитудно-частотной характеристики разомкнутой системы, которому принадлежит частота среза, должен быть равен –20 дБ/дек и  его протяженность должна составлять примерно одну декаду.

          Рассмотрим методику построения границ точности и робастности в графическом окне Open-LoopBodeEditor(C) с изображением логарифмической амплитудно-частотной характеристики разомкнутой системы (рис. 28). Средство SISOTOOL позволяет строить эти границы в виде ломаных линий.

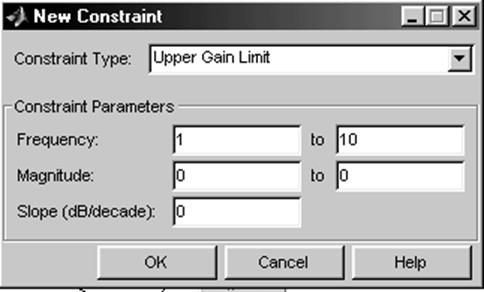
Чтобы построить границу точности:

          а) вызовите меню правой клавиши мыши в графическом  окне      Open-LoopBodeEditor(C) и выберите команду New (новая граница) из подменю     Design Constraints(построить     границы     желаемой     области расположения логарифмической амплитудно-частотной характеристики разомкнутой проектируемой системы). Появляется диалоговое окно NewConstraint  (выбираемые параметры новой границы) (рис. 29), в котором по умолчанию в текстовом окне с названием ConstraintType (вид ограничения) высвечивается UpperGainLimit (верхняя предельная граница);

б) установите в текстовом окне с названием ConstraintTypeс помощью раскрывающегося   списка   режим   LowerGainLimit(нижняяпредельная

граница);

          в) осуществите в поле ConstraintParameters следующие операции:

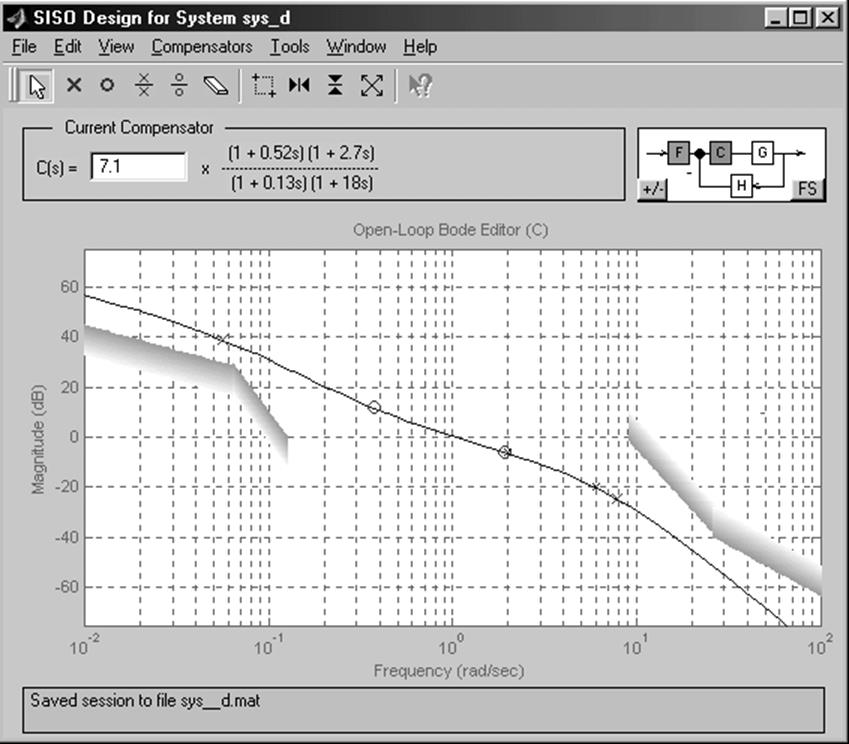
Рис. 28

·  если отсутствует требование астатизма, то введите: в текстовые подокна с общим названием Frequency  соответственно нижнее и верхнее желаемые значения частоты для первого  отрезка границы точности, например значения 0.001 и 0.065, причем верхнее значение  частоты  должно  быть   равно