Программа профильной лаборатории «Учебное исследование в математике», страница 19

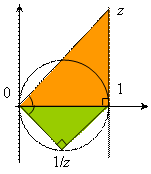
Закрашенные треугольники подобны, поэтому точка 1/z пробегает окружность с центром (½, 0) и радиусом ½.

Задача 6. Найдите преобразование комплексной  плоскости, переводящее верхнюю полуплоскость в единичный круг.

Например, такое: z₁ = z + i, z₂ = 1/z₁, z₃ = 2z₂ + i.

Тема 5. Координатное представление комплексного числа

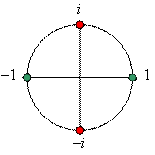
Задача 7. Найдите все комплексные числа z, для которых z² = –1; z² = –4; z² = –3.

Для надёжности перепишем первое равенство в виде пропорции: z² = –1 Þ z² = –1·1 Þ . Стало быть, z так получается из 1, как –1 получается из z. Понятно, что длина z равна 1. Ведь если бы длина z получалась бы из 1 увеличением или уменьшением в a раз, то и длина –1 получалась бы из z таким же увеличением или уменьшением в a раз. Но итоговая длина равна начальной, поэтому a = 1. Стало быть, z лежит на единичной окружности. Далее, за два раза надо повернуться на 180°. Поэтому за один раз надо повернуться на 90°. Впрочем, поворот на –90° тоже подходит.

Для второго и третьего уравнений мы составим аналогичные пропорции , .

Задача 8. Даны комплексные числа z = 1 + i, w = –4 + 2i. Найдите числа z + w, z – w, z · w, z², z³, w : z.

Это те же самые числа, что и в задаче 1, только теперь мы заменили геометрические построения алгебраическими преобразованиями. Техника деления: домножаем числитель и знаменатель на число, сопряжённое со знаменателем.

Задача 9. Вычислите сумму 1 + i + i² + i³ + ... + i¹⁰⁰.

Воспользуемся цикличностью: i⁰ = 1, i¹ = i, i² = –1, i³ = i, i⁴ = 1, i⁵ = i, … . Сумма любой последовательной четвёрки слагаемых равна 0, и поэтому полная сумма равна 1.

Задача 10. Вычислите (1 + i)¹⁰; ( + i)³⁰.

В первом примере (1 + i)¹⁰ = (2i)⁵ = 32i.

Ко второму примеру удобно нарисовать картинку. Направленный отрезок  + i получается из единичного отрезка растяжением в 2 раза и поворотом на 30°. 30 растяжений в 2 раза — это растяжение в 2³⁰ раз. 30 поворотов на 30° — это два полных оборота и ещё поворот на 180°. Поэтому ( + i)³⁰ = 2³⁰ i.

Задача 11. Покажите, что ломаную на рисунке можно неограниченно продолжать так, чтобы углы при всех её вершинах были равны, длины сторон образовывали геометрическую прогрессию, и при этом все вершины находились в узлах клетчатой бумаги.

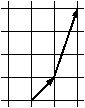
Если углы при вершинах ломаной равны, а длины её сторон образуют геометрическую прогрессию, это означает, что все соседние звенья ломаной имеют между собой одно и то же отношение. Это отношение равно . Первое звено ломаной — это комплексное число с целыми коэффициентами. Каждое следующее звено получается из предыдущего умножением на комплексное число с целыми коэффициентами. Поэтому все звенья ломаной будут комплексными числами с целыми коэффициентами.