Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 6

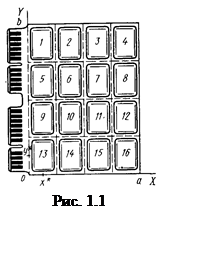
В результате получим фиксированные позиции для установки элементов.

Следует отметить, что перед разбиением поверхности коммутационной платы на позиции из нее, исходя из конструктивных соображений, выделяют области для размещения выводных контактных зон схемы (разъемов), а также запрещенные области, в которых не должны помещаться элементы схемы (зоны крепления платы, конструктивные вырезы и т. п.).

Все конструктивные элементы, подлежащие размещению, можно условно разделить на три группы [1]:

1) нефиксированные элементы, местоположение которых на плате заранее не известно. Пусть таких элементов будет q;

2) граничные элементы, к которым относятся элементы, связанные с разъемами, осуществляющими электрическую связь с элементами, расположенными на других коммутационных платах. Так как разъемы обычно помещают на внешней стороне коммутационной платы (рис. 1.1), то эти элементы желательно располагать у границы коммутационного поля. Пусть число таких элементов будет h — q;

3) фиксированные элементы, местоположение которых на плате заранее определено (указано разработчиком). Таких элементов будет n — h.

Для рассмотренного случая задачу размещения можно сформулировать следующим образом. Найти такое местоположение элементов на коммутационной плате, при котором достигается минимум

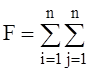c_ij[(x_i - x_j)^t + (y_i - y_j)^t].                 (1.6)

Оптимизацию размещения осуществляют, как правило, локально из некоторого случайного или интуитивно выбранного первоначального размещения.

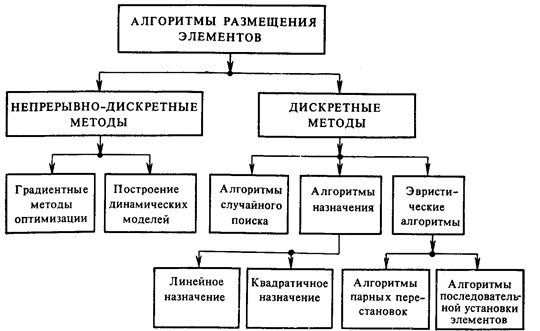
По принципам реализации известные алгоритмы  размещения можно разделить на алгоритмы, использующие непрерывно-дискретные и дискретные методы оптимизации (рис. 1.2). Эффективность того или иного алгоритма обычно оценивают по результатам решения типовых конструкторских задач.

	Рис. 1.2

 

Эвристические алгоритмы. Практическая реализация большинства указанных на рис. 1.2 алгоритмов размещения связана со значительными затратами машинного времени и памяти ЭВМ. Поэтому для размещения большого числа конструктивных элементов (n > 100) часто используют эвристические алгоритмы, позволяющие сократить время решения задачи при вполне приемлемом для практики качестве получаемого результата. Кроме того, такие алгоритмы лучше приспособлены для учета конкретных конструкторско-технологических ограничений. К данной группе алгоритмов относятся итерационные, последовательные и смешанные, в которых начальное размещение получают с помощью последовательного закрепления элементов в позициях, а улучшение размещения достигается в результате их парных перестановок [1].

Итерационные алгоритмы имеют структуру, аналогичную итерационным алгоритмам компоновки, рассмотренным в пункте 1.2. В них для улучшения исходного размещения элементов на плате вводят итерационный процесс перестановки местами пар элементов.

В случае минимизации суммарной взвешенной длины соединений формула для расчета изменения значения целевой функции при перестановке местами элементов r_i и r_j, закрепленных в позициях t_j и t_g, имеет вид [1]

DF_ij(f,g) =(c_ip - c_jp)(d_fh(p) - d_gh(p)),                (1.7)

где р и h(p) — порядковый номер и позиция закрепления неподвижного элемента r_р. Если DF_ij(f, g) > 0, то осуществляют перестановку r_i, и r_j, приводящую к уменьшению целевой функции на DF_ij(f,g), после чего производят поиск и перестановку следующей пары элементов и т. д. Процесс заканчивается получением такого варианта размещения, для которого дальнейшее улучшение за счет парных перестановок элементов невозможно.

Использование описанного направленного перебора сокращает общее число анализируемых вариантов размещения (по сравнению с полным перебором), но приводит к потере гарантии нахождения глобального экстремума целевой функции.

Итерационные алгоритмы позволяют получить локальный экстремум целевой функции, более близкий к глобальному, вследствие учета связей всех размещенных на плате элементов.