Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 42

Определение области Парето осуществляется путем параллельной оптимизации по всем учитываемым критериям методом парных перестановок с помощью рассмотренных выше алгоритмов, а условие реализации перестановки элементов приобретает вид

DF_i ³ 0  i = 1,I.                              (6.21)

Выбор наиболее рационального варианта размещения основывается на информации, поступающей от лица, принимающего решения (ЛПР), т.е. проектировщика. Такая информация о системе предпочтений ЛПР позволяет провести скаляризацию целевой функции путем свертки критериев в виде [19]

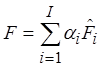,                               (6.22)

где I - число критериев оптимальности;

a_i - весовые коэффициенты;

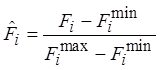;                               (6.23)

где , - минимальное и максимальное значения i-го критерия в области Парето.

Для определения коэффициентов a_i воспользуемся многоуровневым адаптивным алгоритмом, основанным на методах стохастической оптимизации, который позволяет получить свертку критериев с учетом системы предпочтений ЛПР [19].

При использовании такого подхода проводится рандомизация номеров критериев i, для чего вводится дискретная случайная величина v с распределением: P (v = i) = p_i (). Начальные значения вероятностей привлечения i-го критерия устанавливаются равными p_i = 1/I, затем эти вероятности настраиваются на каждом шаге алгоритма с использованием правил локального улучшения. Настройка вероятностей осуществляется в диалоговом режиме с учетом информации, поступающей от ЛПР.

Алгоритм свертки критериев включает выполнение следующих действий.

1⁰ . Оптимизируется размещение элементов на плате по каждому из используемых критериев F_i методом парных перестановок с определением ,, и получаются множества эффективных решений.

2⁰. Рассчитываются  по (6.23).

3⁰.Устанавливаются начальные значения вероятностей p_i = =1/I.

4⁰. Проводится на каждом k-м шаге генерирование случайного числа j, равномерно распределенного на интервале [0,1].

5⁰. Выбирается значение v по следующим условиям: если  j < p₁, то v = 1; если j > p₁ и j < p₁ + p₂, то v = 2 и т.д.

6⁰. Выбирается вариант размещения с оптимальным значением критерия , для которого рассчитываются значения остальных критериев, образующие вектор F^k = {, i <> v}.

7⁰. Указывается ЛПР критерий с номером i = w, имеющий наименее удовлетворительное значение. Это указание формализуется в виде

.

8⁰. Проводится настройка вероятностей p_i для реализации величины v на следующем (k+1)-м шаге:

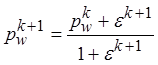,                                (6.24)

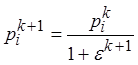,                                (6.25)

,                (6.26)

где 0 < e < 1 - шаг настройки вероятностей.

9⁰. Проверяется условие , где m - число шагов для проверки условия стабилизации значений p_i; g - малая положительная величина. Если условие не выполняется, то переход к 4⁰, иначе - свертка критериев в виде (6.22) с весовыми коэффициентами .

Полученный в результате глобальный критерий используется затем для выбора наиболее предпочтительного варианта размещения.

ЗАКЛЮЧЕНИЕ

Для исследования алгоритмов парных перестановок при решении задач оптимизации компоновки и размещения разработаны и отлажены необходимые алгоритмы и программы, в которых для создания большого количества начальных распределений или размещений использовалась функция рандомизации. Программы разработаны в среде Delphi 3.0 и находятся на кафедре КиПР ВГТУ. Это следующие программы:

1) программа оптимизации компоновки с произвольным начальным распределением;