|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1 |
0 |
5 |
0 |
0 |
0 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
|
2 |
5 |
0 |
8 |
0 |
0 |
0 |
0 |
3 |
2 |
0 |
0 |
0 |
|
3 |
0 |
8 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
2 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
|
5 |
0 |
0 |
0 |
4 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
2 |
3 |
|
7 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
|
8 |
2 |
3 |
0 |
0 |
0 |
0 |
2 |
0 |
4 |
0 |
0 |
0 |
|
9 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
3 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
4 |
0 |
|
11 |
0 |
0 |
0 |
2 |
0 |
2 |
0 |
0 |
0 |
4 |
0 |
4 |
|
12 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
4 |
0 |
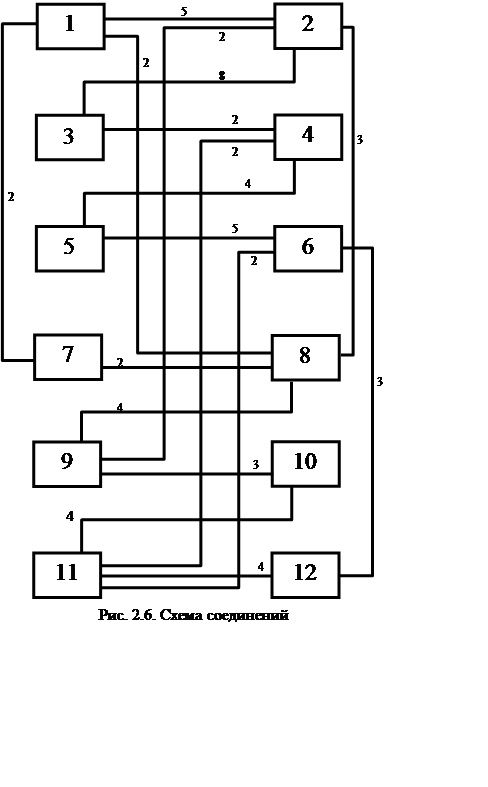
Для данной схемы при следующем произвольном начальном распределении:
|
Блок 1 |
1 |
3 |
4 |
6 |
8 |
11 |
|
Блок 2 |
2 |
5 |
7 |
9 |
10 |
12 |
Число соединений между блоками до оптимизации равно 44.
Результаты работы алгоритма парных перестановок при произвольном начальном распределении, указанном выше; таковы:
|
Блок 1 |
3 |
4 |
5 |
6 |
11 |
12 |
|
Блок 2 |
1 |
2 |
7 |
8 |
9 |
10 |
Число соединений между блоками равно 12.
Результаты работы только алгоритма начального распределения
|
Блок 1 |
2 |
3 |
1 |
8 |
9 |
10 |
|
Блок 2 |
5 |
6 |
4 |
12 |
11 |
7 |
Число соединений между блоками равно 10.
Результаты работы алгоритма парных перестановок с использованием алгоритма начального распределения:
|
Блок 1 |
2 |
3 |
1 |
8 |
9 |
7 |
|
Блок 2 |
5 |
6 |
4 |
12 |
11 |
10 |
Число соединений между блоками равно 5.
 |
Результаты работы алгоритма полного перебора (глобальный оптимум):
|
Блок 1 |
2 |
3 |
1 |
8 |
9 |
7 |
|
Блок 2 |
5 |
6 |
4 |
12 |
11 |
10 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.