Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 5

Поэтому все применяемые в настоящее время алгоритмы размещения используют промежуточные критерии, которые лишь качественно способствуют решению основной задачи: получению оптимальной трассировки соединений. К таким критериям относятся:

1) минимум суммарной взвешенной длины соединений;

2) минимум числа соединений, длина которых больше заданной;

3) минимум числа пересечений проводников;

4) максимальное число соединений между элементами, находящимися в соседних позициях либо в позициях, указанных разработчиком;

5) максимум числа цепей простой конфигурации.

Наибольшее распространение в алгоритмах размещения получил первый критерий, что объясняется следующими причинами: уменьшение длин соединений улучшает электрические характеристики устройства, упрощает трассировку печатных проводников и снижает трудоемкость изготовления печатных плат; кроме того, он сравнительно прост в реализации.

В зависимости от конструкции коммутационной платы и способа выполнения соединений расстояние между позициями установки элементов подсчитывается по одной из следующих формул:

;                   (1.1)

;                      (1.2)

.                     (1.3)

где (х_i, y_i) и (х_j, y_j) — координаты i-й и j-й позиций коммутационной платы. Формула (1.1) соответствует проведению проводников по кратчайшему пути между соединяемыми точками. Выражение (1.2) предполагает раскладку проводников по каналам или магистралям, параллельным сторонам платы, что характерно для печатного монтажа с ортогональным рисунком соединений и жгутового монтажа.

Формулу (1.3) применяют при наличии особых требований к максимальной длине отдельных соединений (как правило, t = 2).

При практической реализации алгоритмов размещения часто используют представление конструктивных элементов и позиций на коммутационной плате точками, совпадающими с их геометрическими центрами, а все соединения между элементами приводят к попарно взвешенным связям. Весовые оценки связей учитывают такие характеристики схемы, как число электрических цепей между элементами, теплонагруженность элементов, условия распространения сигналов в цепях и т. д. Широкий класс таких оценок описывается формулой [1]:

,                               (1.4)

где  — вес s-й цепи, связывающей элементы i и j; x(r_s) — коэффициент учета размера цепи, равный 2/r_s; r_s — число эквипотенциальных выводов s-й цепи; g — число цепей, связывающих элементы i и j. Величина  определяет важность s-й цепи с точки зрения минимизации ее длины (при работе алгоритма в первую очередь минимизируются связи с большим весом).

Если при решении задач размещения требуется произвести рассредоточение теплонагруженных элементов, то

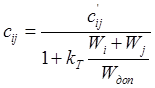                              (1.4a)

где  - значение коэффициента взвешенности, определяемое из соотношения (1.4); W_i и W_j - мощности рассеяния соответственно i-го и j-го элементов; W_доп - допустимая мощность рассеяния двух рядом стоящих элементов; k_T - коэффициент, учитывающий теплоотдачу в реальной конструкции. Аналогичным образом можно учесть электромагнитную совместимость элементов на плате.

В общем виде задача размещения конструктивных элементов на коммутационной плате формулируется следующим образом. Задано множество конструктивных элементов R = {r₁, r₂,.…,r_n} и множество связей между этими элементами V = {v₁,v2, ..., v_p}, а также множество установочных мест  (позиций) на коммутационной   плате T = {t₁, t₂, ..., t_k}. Найти такое отображение множества R на множестве Т, которое обеспечивает экстремум целевой функции F.

Если критерием качества размещения является минимум суммарной взвешенной длины соединений, то задача состоит в минимизации

                                   (1.5)

Как указывалось ранее, наиболее часто решение задачи ищется именно в такой постановке.

Обычно поле позиций (коммутационная плата) имеет форму прямоугольника Р_ab = а ´ b с координатами 0£x£а и          0 £ y £b. Вся площадь платы разбивается на ряд областей (позиций), число которых должно быть не меньше числа размещаемых элементов (рис. 1.1).