После этого аналогичные действия производим для блоков Хg и Хa. Вычислим значения DF для модулей этих блоков.
![]()
= ( 3 + 3 ) - ( 5 + 0 ) - 2 × 3 = - 5;
![]()
= ( 3 + 4 ) - ( 5 + 0 ) - 2 × 0 = 2;
![]()
= ( 3 + 4 ) - ( 5 + 0 ) - 2 × 0 = 2;
![]()
= ( 4 + 3 ) - ( 4 + 0 ) - 2 × 0 = 3;
![]()
= ( 4 + 4 ) - ( 4 + 0 ) - 2 × 4 = - 4;
![]()
= ( 4 + 4 ) - ( 4 + 0 ) - 2 × 0 = 4;
![]()
= ( 4 + 3 ) - ( 9 + 0 ) - 2 × 0 = - 2;
![]()
= ( 4 + 4 ) - ( 9 + 0 ) - 2 × 0 = - 1;
![]()
= ( 4 + 4 ) - ( 9 + 0 ) - 2 × 4 = - 9.
В результате вычислений получим, что для четырех пар модулей
DF > 0. Теперь находим пару модулей,
для которой DF = max. Этой парой
является ![]() , для которой DF = 4, что означает уменьшение количества
межблочных соединений на четыре при перестановке местами этих модулей. Распределение
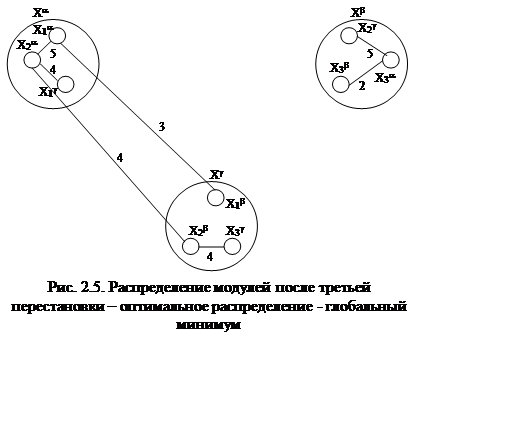
модулей после этой (третьей) перестановки показано на рис. 2.5. Количество
межблочных соединений стало 11 - 4 = 7. Как показывают
вычисления, для схемы рис. 2.5 все DF
< 0, то есть перестановки не целесообразны, что означает достижение
оптимизации между всеми блоками.
, для которой DF = 4, что означает уменьшение количества
межблочных соединений на четыре при перестановке местами этих модулей. Распределение
модулей после этой (третьей) перестановки показано на рис. 2.5. Количество
межблочных соединений стало 11 - 4 = 7. Как показывают
вычисления, для схемы рис. 2.5 все DF
< 0, то есть перестановки не целесообразны, что означает достижение
оптимизации между всеми блоками.
Таким образом в результате оптимизации с помощью алгоритма парных перестановок количество межблочных соединений уменьшилось с 22 (в исходном распределении) до 7 (в оптимальном распределении), то есть более, чем в 3 раза.
 |
2.2. Алгоритм начального распределения
При решении задачи оптимизации используют алгоритм парных перестановок [1,2]. Согласно этому алгоритму, все элементы схемы произвольным образом распределяются по заданному количеству блоков, а затем производятся перестановки тех пар элементов, находящихся в разных блоках, которые дают уменьшение числа межблочных соединений. В результате таких перестановок достигается локальный минимум. Близость его к глобальному минимуму, т.е. степень оптимизации, существенно зависит от начального (исходного) распределения элементов между блоками. Поэтому вместо произвольного начального распределения элементов между блоками лучше вводить простой, но эффективный алгоритм начального распределения, способствующий оптимизации. Он состоит в следующем:
в составленной матрице соединений выбирается максимальное число (а если их несколько, то одно из них) и номера соответствующих элементов заносятся в список элементов первого блока;
в строках или столбцах, соответствующих записанным элементам выбирается еще одно (кроме уже выбранного) максимальное число, и номер элемента, соответствующий этому числу, заносят также в список элементов первого блока, эту операцию повторяют до заполнения первого блока;
если число блоков два, то оставшиеся элементы заносят в список элементов второго блока;
если же число блоков более двух, то, вычеркнув столбцы и строки, соответствующие внесенным в список первого блока элементам, получают новую матрицу;
в этой матрице аналогичным образом выбирают максимальное число и формируют список элементов второго блока;
если число блоков три, то оставшиеся элементы вносят в список элементов третьего блока;
если же число блоков более трех, то, вычеркнув строки и столбцы, соответствующие распределенным элементам, получают еще одну матрицу, с которой выполняют аналогичные операции до полного распределения всех элементов схемы.
Применим для решения задачи, рассмотренной в разд. 2.1, алгоритм начального распределения. Для этого по матрице соединений (табл. 2.1) или просто по схеме выбираем пару модулей, имеющих максимальное число соединений между собой. Этими модулями будут модули x1a и x2a , их заносим в список первого блока (xa). Далее, к этим двум модулям добавляем еще один модуль, имеющий с одним из модулей, занесенных в список блока xa, максимальное число соединений. Им является модуль x1g (4 связи) или x2b (тоже 4 связи).
При выборе модуля x1g получаем в блоке Хa модули x1a, x2a и x1g, то есть имеем уже оптимальный вариант (рис. 2.5). Если же выбираем модуль x2b, то получаем вариант, образующийся после двух парных перестановок (рис. 2.4), то есть общее число перестановок сокращается с трех до одной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.