В тех случаях, когда всю схему надо разбить на 4 одинаковых по количеству модулей блоков, можно сначала произвести разбиение всей схемы на 2 блока, а затем разбить каждый из полученных блоков еще на 2 блока.
В том случае, когда в каком-либо блоке есть вакансии (т.е. свободные места для модулей), можно делать несимметричные перестановки, т.е. переставляют один модуль в тот блок, где есть вакансия, а взамен модуль не ставится. Для несимметричных перестановок :
DF’ = mia - zia.
Если DF’ > 0, то перестановка целесообразна.
Рассмотрим приведенный способ оптимизации соединений между блоками на примере.
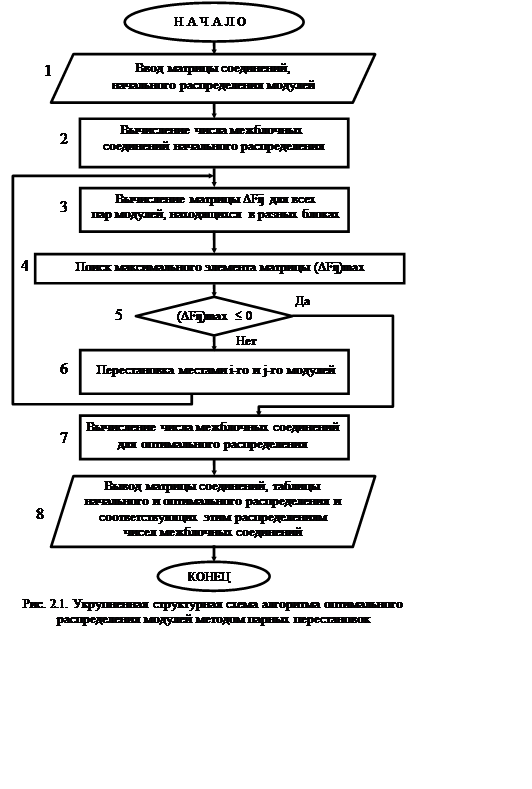
Пусть какое - либо устройство состоит из 9 модулей. Их предварительно каким - либо способом ( например, произвольным способом ) разбили на 3 блока по 3 модуля в каждом блоке (рис. 2.2): в блоке Хa : модули Х1a , Х2a , Х3a;
в блоке Хb : модули Х1b , Х2b , Х3b;
в блоке Хg : модули Х1g , Х2g , Х3g;
На рис. 2.2 – 2.5 цифра у линии соединения модулей показывает количество межмодульных соединений. Общее количество межблочных соединений в исходном состоянии (до оптимизации) равно 22 (рис. 2.2).
Произведем сначала оптимизацию межблочных соединений между блоком Хa и Хb. Для этого вычислим значения DF для всех пар модулей, расположенных в блоках Хa и Хb:
![]()
=( 3 + 3 ) - ( 5 + 0 ) - 2 × 3 = -5;
![]()
=( 3 + 4 ) - ( 5 + 0 ) - 2 × 0 = 2;
![]()
=( 3 + 2 ) - ( 5 + 0 ) - 2 × 0 = 0;
 |
![]()
=( 4 + 3 ) - ( 5 - 0 ) - 2 × 0 = 2;
![]()
= ( 4 + 4 ) - ( 5 + 0 ) - 2 × 4 = - 5;
![]()
= ( 2 + 3 ) - ( 0 + 0 ) - 2 × 0 = 5;
![]()
= ( 2 + 4 ) - ( 0 + 0 ) - 2 × 0 = 6;
![]()
= ( 2 + 2 ) - ( 0 + 0 ) - 2 × 2 = 0.
Получили, что для 5 пар модулей DF > 0. Теперь находим пару, для которой DF = max. Этой парой будет ![]()
![]() ,
для которой DF = 6, т.е. перестановка
,
для которой DF = 6, т.е. перестановка ![]() и
и ![]() местами дает уменьшение
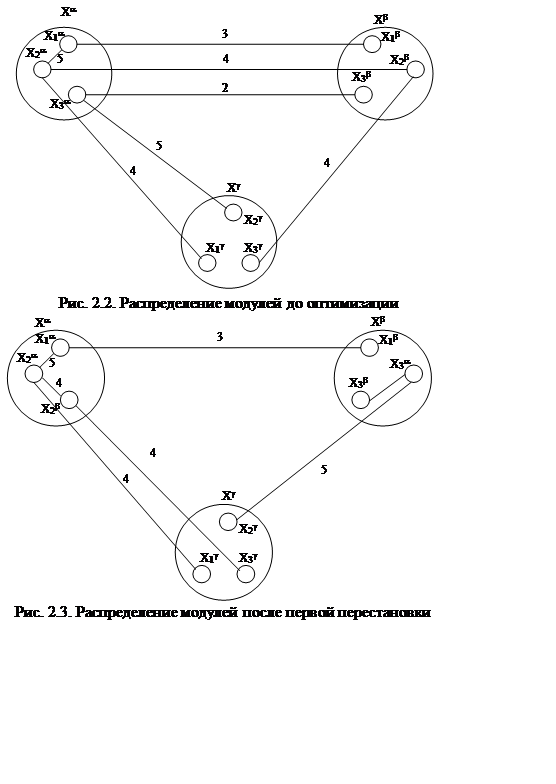
количества связей на 6. Распределение модулей после первой перестановки
показано на рис. 2.3. Количество межблочных связей стало равным 22 - 6 = 16.
Чтобы производить оптимизацию дальше, необходимо вычислить все функционалы для
модулей блоков Хa, Хb (рис. 2.3).
местами дает уменьшение
количества связей на 6. Распределение модулей после первой перестановки
показано на рис. 2.3. Количество межблочных связей стало равным 22 - 6 = 16.
Чтобы производить оптимизацию дальше, необходимо вычислить все функционалы для
модулей блоков Хa, Хb (рис. 2.3).
![]()
= ( 3 + 3 ) - ( 5 + 0 ) - 2 × 3 = -5;
![]()
= ( 3 + 0 ) - ( 5 + 2 ) - 2 × 0 = - 4.
 |
![]()
= ( 3 + 0 ) - ( 5 + 2 ) - 2 × 0 = - 4;
![]()
= ( 0 + 3 ) - ( 4 + 0 ) - 2 × 0 = - 1;
![]()
= ( 0 + 0 ) - ( 4 + 2 ) - 2 × 0 = - 6;
![]()
= ( 0 + 0 ) - ( 4 + 2 ) - 2 × 0 = - 6;
![]()
= ( 0 + 3 ) - ( 9 + 0 ) - 2 × 0 = - 6;
![]()
= ( 0 + 0 ) - ( 9 + 2 ) - 2 × 0 = - 11;
![]()
= ( 0 + 0 ) - ( 9 + 2 ) - 2 × 0 = - 11.
Все вычисленные DF < 0, это означает, что перестановки пар модулей, находящихся в блоке Хa и Хb, нецелесообразны, то есть оптимизация между этими блоками достигнута.
Теперь проведем оптимизацию межблочных соединений между блоком Хb и Хg. Для этого вычислим DF для всех пар модулей, находящихся в блоках Хb и Хg (рис. 2.3).
![]()
= ( 0 + 0 ) - ( 0 + 0 ) - 2 × 0 = 0;
![]()
= ( 0 + 5 ) - ( 0 + 0 ) - 2 × 0 = 5;
![]()
= ( 0 + 0 ) - ( 0 + 0 ) - 2 × 0 = 0;
![]()
= ( 5 + 0 ) - ( 2 + 0 ) - 2 × 0 = 3;
![]()
= ( 5 + 5 ) - ( 2 + 0 ) - 2 × 5 = - 2;
![]()
= ( 5 + 0 ) - ( 2 + 0 ) - 2 × 0 = 3;
![]()
= ( 0 + 0 ) - ( 2 + 0 ) - 2 × 0 = - 2;
![]()
= ( 0 + 5 ) - ( 2 + 0 ) - 2 × 0 = 3;
![]()
= ( 0 + 0 ) - ( 2 + 0 ) - 2 × 0 = - 2.
В результате вычислений получили, что для четырех пар
модулей DF > 0. Теперь находим ту
пару модулей, для которой DF = max.
Этой парой является пара ![]() , для которой
DF = 5, что означает уменьшение
количества межблочных соединений на 5 при перестановке местами этих модулей. Распределение
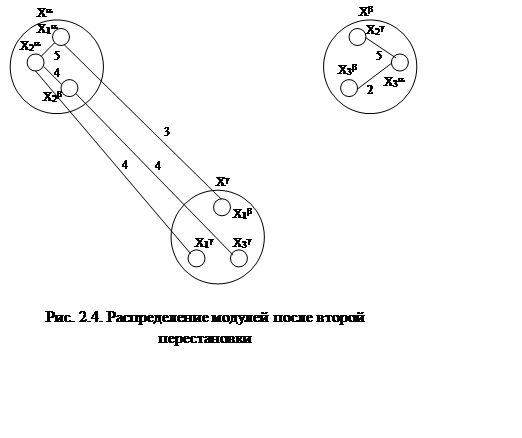
модулей после этой (второй) перестановки показано на рис. 2.4. Общее количество
межблочных соединений уменьшилось еще на пять и стало равным 16 - 5 = 11.
, для которой
DF = 5, что означает уменьшение
количества межблочных соединений на 5 при перестановке местами этих модулей. Распределение
модулей после этой (второй) перестановки показано на рис. 2.4. Общее количество
межблочных соединений уменьшилось еще на пять и стало равным 16 - 5 = 11.
По рис. 2.4 видно, что число межблочных соединений между блоками Хb и Хg равно 0, то есть оптимизация между этими блоками достигнута. Достижение оптимизации между блоками Хb и Хg можно проверить и вычислением всех DF, которые будут меньше или равны нулю (рис. 2.4).
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.