Наилучшее размещение модулей представлено в табл. 3.5.
Минимальная суммарная длина (глобальный минимум) при данном размещении равна 126 единиц.
Особенности результатов решения.
В результате оптимизации с помощью алгоритма парных перестановок 10000 различных исходных размещений получили 35 различных минимумов суммарных длин, различающихся в 1,3 раза, что означает существенную зависимость значения минимума от исходного начального размещения.
Гистограмма распределения этих 35 минимумов с указанием их значений Wi min и вероятности появления каждого из них Pi приведена на рис. 3.7.
Значение глобального минимума Wo min равно 126 единиц длины. Оптимальное размещение элементов для глобального минимума показано в табл. 3.5.
По результатам исследований можно отметить следующее:
1) При оптимизации любого исходного начального размещения элементов суммарная длина соединений уменьшается по сравнению с неоптимизированным в 1,3 - 3 раза.
2) Степень оптимизации, т.е. значение минимума суммарной длины соединений, в значительной степени зависит от начального размещения элементов в установочных позициях (рис. 3.7).
3) Значение суммарной вероятности 
в зависимости от величины 
, показывающей насколько
процентов полученный результат оптимизации отличается от глобального, монотонно
возрастает, асимптотически приближаясь к единице при значениях h, равных 18-22 % (рис. 3.8). По этому
рисунку можно определить суммарную вероятность появления результата
оптимизации, отличающегося от глобального на заданное значение h в процентах. Суммарная вероятность åPi - это сумма вероятностей i-го и всех предыдущих
(лучших) минимумов.
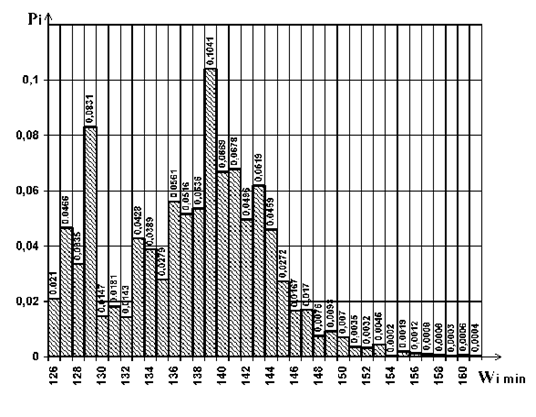
Рис. 3.7. Гистограмма распределения минимумов суммарной длины с указанием вероятности их появления
Таким образом проведенные исследования показали, что степень оптимизации размещения с помощью алгоритма парных перестановок в значительной мере зависит от исходного начального размещения элементов в позициях и, чтобы результат оптимизации приближался к глобальному минимуму, необходимо проводить оптимизацию для нескольких (не менее 10-20) исходных начальных размещений и из полученных результатов выбрать лучший. Это один из способов повышения эффективности алгоритма парных перестановок [15].
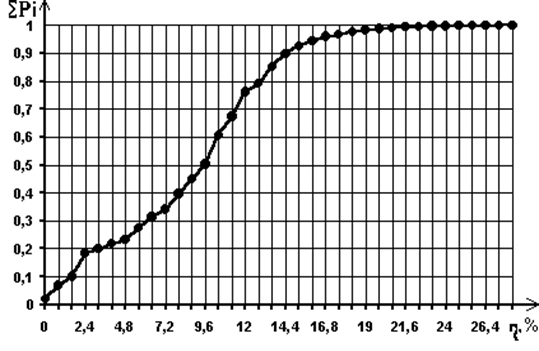
Рис. 3.8. Вероятность появления результата оптимизации, отличающегося от глобального не более, чем на h процентов
Вторым способом является метод, в алгоритме которого из всех возможных целесообразных перестановок пар элементов выбирается та пара элементов, перестановка которых дает максимальное уменьшение суммарной длины соединений, а не первая попавшаяся целесообразная перестановка. Как показали наши исследования, при этом методе вероятность появления минимумов, расположенных ближе к глобальному, возрастает, а самых удаленных - уменьшается (рис. 3.7).
4. АЛГОРИТМ ПАРНЫХ ПЕРЕСТАНОВОК
ДЛЯ ОПТИМИЗАЦИИ РАЗМЕЩЕНИЯ С МИНИМИЗАЦИЕЙ ЧИСЛА ПЕРЕСЕЧЕНИЙ ПРОВОДНИКОВ
4.1. Метод парных перестановок
При автоматизированном размещении элементов обычно в качестве критерия оптимизации выбирается минимум суммарной длины соединений, дающий ряд положительных эффектов: повышение надежности, снижение паразитных взаимосвязей и т.д. Наряду с этим критерием оптимизации предлагается при решении задачи оптимального размещения использовать и такой критерий, как минимум числа пересечений проводников, приводящий к уменьшению числа проволочных перемычек, к упрощению формы печатных проводников, к уменьшению суммарной длины, что в конечном итоге ведет к уменьшению трудоемкости изготовления изделия, снижению себестоимости, увеличению надежности соединений, снижению паразитных взаимосвязей и упрощению трассировки соединений.
Для иллюстрации решения этой задачи представим схему в виде графа (рис. 4.1), в котором вершинами являются элементы (модули) схемы, а ребрами – соединения между элементами. Размещение позиций, в которые устанавливаются вершины графа, задается их координатами x и y, а соединения между элементами задаются матрицей связей (табл. 4.1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.