Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 35

При формировании критериев оптимальности F_т могут применяться различные характеристики температурного поля, главными из которых являются: локальный перегрев в заданной точке; максимальный перегрев; суммарный перегрев; средний перегрев; равномерность температурного поля по подложке (плате, кристаллу); разность максимального и минимального перегревов; перепад температур между заданными точками; градиент температуры.

Выбор конкретных критериев осуществляется с учетом функционального назначения и конструкции РЭС.

Вычисление значений перегревов будем проводить с использованием аналитических моделей температурного поля пластины с поверхностными источниками тепла [12,13].

Двумерное стационарное распределение перегрева в пластине  находят путем решения уравнения

 , (6.2)

где ,  - размеры пластины (см. рис. 6.1);

d - толщина пластины;

l_х, l_у - эффективные теплопроводности в направлении           осей х и у;

a - сумма коэффициентов теплоотдачи с обеих сторон боковой поверхности (a = const);

q(х, у) - поверхностная плотность теплового потока от локальных источников, равная нулю вне зон расположения источников и постоянная в пределах зоны действия каждого i-го источника:

;                          (6.3)

.

Во многих практически важных случаях теплоотдачей с торцов можно пренебречь по сравнению с теплоотдачей на боковой поверхности и тогда граничные условия имеют вид

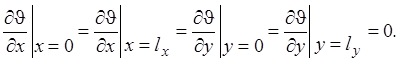   (6.4)

При граничных условиях (6.3), (6.4) перегрев рассчитывается по формуле

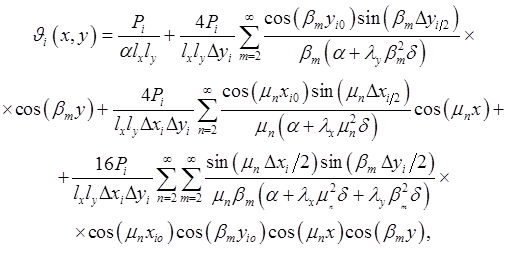 (6.5)

где , ;

P_i – мощность тепловыделения i-го элемента (источника тепла);

Dx_i, Dy_i – размеры элемента r_i;

x_i0, y_i0 – координаты центра элемента r_i.

При вычислении собственного перегрева i-го элемента (J_ii) координаты расчетной точки совпадают с центром данного элемента (x = x_i0, y = y_i0). В случае определения наведенного перегрева от i-го элемента на j-й (J_ij) в качестве координат центра источника тепла используются координаты i-го элемента (x_i0, y_i0), а для расчетной точки – координаты центра j-го элемента (x = x_j0, y = y_j0).

Рассмотрим решение подобных задач размещения для наиболее эффективных и широко применяемых критериев F₁,F₂, и F₃ (средний перегрев элементов на плате, среднеквадратическое отклонение перегревов от среднего и локальный перегрев):

                           (6.6)

                  (6.7)

.                               (6.8)

Так как локальный перегрев, как это следует из (6.6) и (6.8), является частным случаем критерия F₁ , то в дальнейшем будем рассматривать методы оптимизации для F₁, принимая во внимание, что полученные результаты справедливы и для локальных перегревов.

Рассмотрим наиболее общий случай, когда РЭС характеризуется отсутствием фиксированных позиций для размещения, но все элементы или выделенные группы элементов возможно считать одногабаритными.

Для решения данной задачи разделим её на две подзадачи: получение начального размещения и улучшение начального размещения итерационными методами.

Для получения начального варианта размещения необходимо осуществить разбиение множества Е на множества Е_m, m=1, M (ÈE_m=E, ÇЕ_m=Æ, |Е_m| = N_m), так чтобы выполнялось условие

|q_k-q_j|®min,                                     (6.9)

где 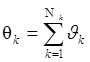, 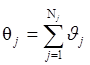- суммарные перегревы элементов, включенных в множества Е_k и Е_j.

Формирование начального размещения осуществляется с использованием предложенного способа [14], основанного на применении модифицированного метода дихотомического деления [17].

Такой способ повышает равномерность размещения тепловыделяющих элементов или их групп (из 5 - 20 элементов) на поверхности платы, что предотвращает появление локально перегруженных участков, что, в свою очередь, повышает надежность и устойчивость работы изделия в целом.

Предлагаемый алгоритм работает следующим образом. Массив из N элементов, имеющих различные перегревы, т.е. различную температуру, нами разбивается на практически одинаковые по количеству элементов группы с примерно одинаковой суммарной температурой. Эти группы элементов размещаются на коммутационном поле (КП) в соответствующих областях КП.