Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 14

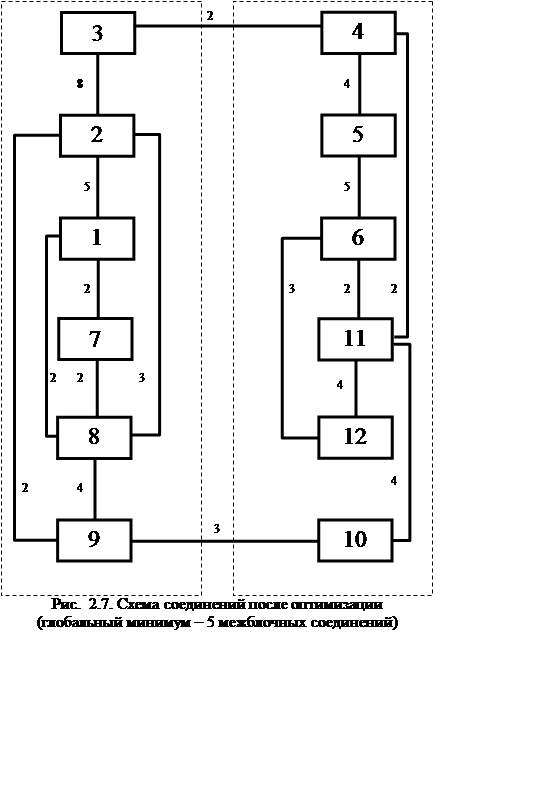
Число соединений между блоками равно 5 (рис. 2.7.)

Вывод : алгоритм парных перестановок с использованием алгоритма начального распределения дал глобальный оптимум, что подтверждается результатами работы алгоритма полного перебора.

2.3. Исследование зависимости эффективности

 алгоритма парных перестановок от исходных начальных распределений и пути повышения его эффективности

Как отмечалось в разд. 1.1. результаты оптимизации компоновки с помощью алгоритма парных перестановок существенно зависят от исходного начального (обычно произвольного) распределения элементов между блоками. В связи с этим целесообразно исследовать зависимость степени оптимизации компоновки РЭА с помощью алгоритма парных перестановок от начального распределения. Для этого необходимо разработать программу, реализующую алгоритм парных перестановок с использованием большого количества начальных распределений. Для каждого начального распределения должна быть проведена своя оптимизация. Для создания большого количества распределений можно использовать функцию рандомизации, включив эту функцию в программу. Для облегчения обработки статистических данных в программе следует предусмотреть вывод результатов оптимизации в порядке уменьшения степени оптимизации с указанием количества появлений каждого оптимума. Отдельно вывести наилучший оптимум с матрицей распределения элементов по блокам. Для оценки степени оптимизации необходимо сравнить локальный оптимум с глобальным. Для получения или проверки наличия глобального оптимума составить программу полного перебора.

Поставленные задачи были нами решены.

1. Разработана программа оптимального распределения элементов с получением большого количества (1000-10000) исходных начальных распределений методом рандомизации;

Для создания начального распределения методом рандомизации была написана подпрограмма, работающая следующим образом.

а) в цикле заполняем промежуточную матрицу именами элементов по возрастанию;

б) для введения случайного фактора выбора ячейки промежуточной матрицы подключаем процедуру RANDOMIZE языка PASCAL;

в) организуем цикл по проходу всех блоков и всех элементов в блоке.

В этом цикле промежуточной переменной q присваиваем случайное значение с помощью функции RANDOM языка PASCAL, имеющей в качестве параметра общее количество элементов в блоках, а затем увеличиваем значение q на 1, так как функция RANDOM возвращает значение в пределах ( 0 <= возвращаемое значение < параметр ). Если не увеличить значение переменной q на 1, то произойдет обращение к нулевому элементу промежуточной матрицы, который содержит ошибочную информацию и не произойдет обращение к последнему элементу матрицы, т.е. мы потеряем одно имя элемента из промежуточной матрицы, что приведет к ошибке.

г) далее организуем поиск в промежуточной матрице имен элементов, которые не равны нулю т.к. у нас нет элементов с именем 0, а в матрице могут находиться нули;

д) если найденное имя элемента не равно нулю, то присваиваем его элементу матрицы распределения;

е) заменяем данное имя элемента в промежуточной матрице нулем, чтобы исключить возможное повторное считывание этого имени и повторной записи его в матрицу распределения, что вызовет ошибку.

2. Разработана программа, реализующая алгоритм полного перебора для проверки глобальности оптимума, получаемого в результате работы алгоритма парных перестановок с рандомизацией начального распределения.

Исследования проводились на пяти различных схемах соединений с использованием 1000 - 10000 исходных начальных распределений для каждой схемы.

Рассмотрим несколько контрольных примеров и дадим анализ их результатов.

Контрольный пример № 1

Исходные данные:

количество элементов = 12;

количество блоков = 2;

количество элементов в блоке 1 = 6;

количество элементов в блоке 2 = 6;

количество начальных распределений = 1000.

матрица связей: