Алгоритм парных перестановок для решения задач оптимизации компоновки и размещения элементов РЭС: Учебное пособие, страница 33

2) Степень оптимизации, т.е. значение минимума пересечений, в значительной степени зависит от начального размещения элементов в установочных позициях (рис. 4.12).

3) Значение суммарной вероятности  в зависимости от величины , показывающей насколько процентов полученный результат оптимизации отличается от глобального, монотонно возрастает, асимптотически приближаясь к единице при значениях h, равных 290-300 % (рис. 4.13). По этому рисунку можно определить суммарную вероятность появления результата оптимизации, отличающегося от глобального на заданное значение h в процентах. Суммарная вероятность åPi - это сумма вероятностей i-го и всех предыдущих (лучших) минимумов.

4) Наилучшее размещение (глобальный минимум) приведено в табл. 4.6.

Таблица 4.6

5) Гистограмма распределения этих 24 минимумов с указанием их значений S_imin и вероятности появления каждого из них P_i приведена на рис. 4.12. По оси Х отложены значения минимумов S_{i min}, а по оси Y - вероятность P_i их появления.

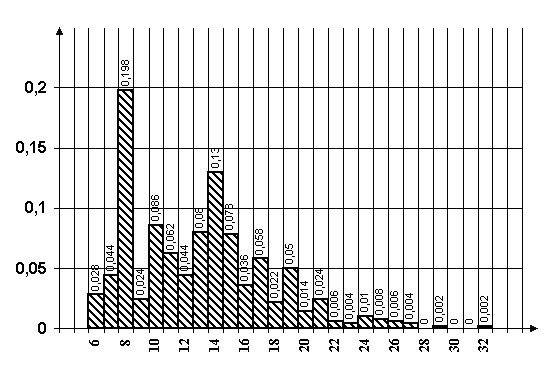
Рис. 4.12. Гистограмма распределения минимумов числа пересечений с указанием вероятности их появления.

Таким образом проведенные исследования показали, что степень оптимизации размещения с помощью алгоритма парных перестановок в значительной мере зависит от исходного начального размещения элементов в позициях, и, чтобы результат оптимизации приближался к глобальному минимуму, необходимо проводить оптимизацию для нескольких (не менее 10-20) исходных начальных размещений и из полученных результатов выбрать лучший. Это один из способов повышения эффективности алгоритма парных перестановок.

Вторым способом является метод, в алгоритме которого из всех возможных целесообразных перестановок пар элементов выбирается та пара элементов, перестановка которых дает максимальное уменьшение суммарной длины соединений, а не первая попавшаяся целесообразная перестановка. Как показали наши исследования, при этом методе вероятность появления минимумов, расположенных ближе к глобальному (рис. 4.12), возрастает, а самых удаленных – уменьшается.

5. ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ ПО ДВУМ КРИТЕРИЯМ

При оптимизации размещения элементов по критерию минимума суммарной длины получаем такие положительные эффекты, как снижение трудоемкости изготовления и количества используемого провода при проводном монтаже, повышение надежности соединений, снижение паразитных емкостей и взаимосвязей и некоторые другие. При оптимизации размещения по критерию минимума числа пересечений получаем такие положительные эффекты, как уменьшение числа проволочных перемычек, упрощение формы печатных проводников, что в конечном итоге ведет к уменьшению трудоемкости изготовления изделия, снижению себестоимости, увеличению надежности изделия, упрощению трассировки соединений. В связи с указанным целесообразно провести оптимальное размещение элементов на коммутационном поле, оптимизированное сразу по обоим указанным выше критериям. Рассмотрим некоторые варианты такой оптимизации.

Во-первых, можно провести оптимальное размещение с минимизацией суммарной длины, найти самое оптимальное размещение по этому критерию, а потом провести оптимизацию по критерию минимизации числа пересечений, то есть получить последовательную оптимизацию по двум критериям. Но, как показывают наши исследования, размещение, полученное при оптимизации по критерию минимума суммарной длины, значительно ухудшается последующей оптимизацией по критерию минимума пересечений.

То же самое происходит, если провести сначала оптимизацию по критерию минимума пересечений, а затем по критерию минимизации суммарной длины соединений.