U(ti+1) = U(ti) + Δsign[U(ti+1) – U(ti)], (14.22)
где «знаковая» функция sign(x) равна +1 при х > 0 и –1 для х < 0.
 При
правильно выбранных периоде дискретизации Tт
и шаге квантования ∆ сигнал R(t) как бы следит за сигналом r(t) при этом ошибка квантования ξ(t) = r(t) – R(t)всегда меньше ∆ по модулю (см. рис. 14.12, г).
При очень резких изменениях сигнала r(t)слежение может
происходить так, как показано на рис. 14.14, а. При этом R(t) будет значительно отличаться
от r(t), и ошибка квантования превысит ∆. Ошибки
такого вида называют шумом перегрузки. Цифровой сигнал при
перегрузке показан на рис. 14.14, б. Он представляет собой
последовательность единиц одного знака, тогда как при нормальном режиме (см.
рис. 14.12, 6) сигнал g(t) состоит из чередующихся по знаку
единиц. На практике в линию поступает последовательность символов 1 и 0, т.е.
символы «–1» преобразуют в 0, а на приемной
стороне перед интегратором производят обратное преобразование.
При
правильно выбранных периоде дискретизации Tт
и шаге квантования ∆ сигнал R(t) как бы следит за сигналом r(t) при этом ошибка квантования ξ(t) = r(t) – R(t)всегда меньше ∆ по модулю (см. рис. 14.12, г).
При очень резких изменениях сигнала r(t)слежение может
происходить так, как показано на рис. 14.14, а. При этом R(t) будет значительно отличаться
от r(t), и ошибка квантования превысит ∆. Ошибки
такого вида называют шумом перегрузки. Цифровой сигнал при
перегрузке показан на рис. 14.14, б. Он представляет собой
последовательность единиц одного знака, тогда как при нормальном режиме (см.
рис. 14.12, 6) сигнал g(t) состоит из чередующихся по знаку
единиц. На практике в линию поступает последовательность символов 1 и 0, т.е.
символы «–1» преобразуют в 0, а на приемной
стороне перед интегратором производят обратное преобразование.
 Отставание
R(t) от r(t) можно умень шить за счет повышения
тактовой частоты Fт = 1/Tт или за счет увеличения шага квантования ∆.
Возрастание Fт невыгодно
с точки зрения построения линейного тракта, увеличение ∆ приводит к росту шумов
квантования. Для выбора компромиссных значений ∆ и Fт необходимо произвести количественный
анализ процессов при ДМ.
Отставание
R(t) от r(t) можно умень шить за счет повышения
тактовой частоты Fт = 1/Tт или за счет увеличения шага квантования ∆.
Возрастание Fт невыгодно
с точки зрения построения линейного тракта, увеличение ∆ приводит к росту шумов
квантования. Для выбора компромиссных значений ∆ и Fт необходимо произвести количественный
анализ процессов при ДМ.
Скорость изменения входного сигнала равна S(t) = dr(t)/dt. Соответственно за время Tт сигнал r(t) изменяется на величину ∆r(t) = TтS(t). Изменение ∆R отслеживающего сигнала R(t) равно шагу квантования ∆. Во избежание ошибки отслеживания (шумов перегрузки) необходимо, чтобы ∆R > ∆r. Труднее всего обеспечить это условие при передаче наиболее сильного абонента rб(t) в моменты времени, когда его скорость изменения принимает максимальное значение Sпик.б. Отсюда следует, что для любого абонента в системе ДМ будут отсутствовать шумы перегрузки, если выполнено условие
Sпик.бTт ≤ ∆. (14.23)
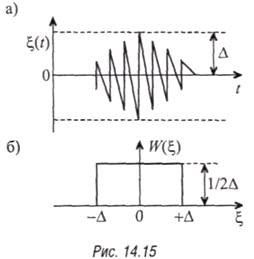 В этом
случае основным источником искажений (шума) сигнала r(t) на
выходе декодера будет шум квантования ξ(t) = r(t) – R(t). Типичная форма процесса ξ(t), который нетрудно построить
непосредственно, например, по рис. 14.12, г, показана на рис. 14.15, а.
Размах ξ(t) не превышает ∆. Закон
распределения мгновенных значений W(ξ) процесса ξ(t), как правило, полагают
равномерным на интервале [–∆; +∆] (рис. 14.15, б). В этом случае
дисперсия сигнала ξ(t) до дискретизации определяется так же, как в
параграфе 12.3:
В этом
случае основным источником искажений (шума) сигнала r(t) на
выходе декодера будет шум квантования ξ(t) = r(t) – R(t). Типичная форма процесса ξ(t), который нетрудно построить
непосредственно, например, по рис. 14.12, г, показана на рис. 14.15, а.
Размах ξ(t) не превышает ∆. Закон
распределения мгновенных значений W(ξ) процесса ξ(t), как правило, полагают
равномерным на интервале [–∆; +∆] (рис. 14.15, б). В этом случае
дисперсия сигнала ξ(t) до дискретизации определяется так же, как в
параграфе 12.3:
 .
.
Учитывая условия нормировки
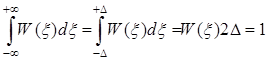 , получим W(ξ) = 1/2∆ и соответственно
, получим W(ξ) = 1/2∆ и соответственно
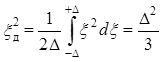 .
.
Отношение сигнал—шум квантования на выходе системы ДМ находим с учетом того, что шум квантования имеет протяженный спектр (см. рис. 14.15, а) и после дискретизации во времени он «свернется» в область частот, равную половине частоты дискретизации. По аналогии с материалом параграфа 12.3 получим уточненное выражение
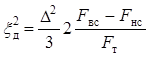 .
(14.24)
.
(14.24)
Отношение сигнал—шум квантования на выходе системы равно
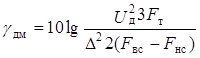 .
(14.25)
.
(14.25)
В выражениях (14.24), (14.25) Fвс, Fнс— верхняя и нижняя частота спектра сигнала, пропускаемая фильтром нижних частот, стоящим на выходе демодулятора; Uд — действующее напряжение сигнала r(t).
Для определения величины ∆ используем условие (14.23). Самая большая скорость изменения сигнала будет у самого сильного (большого) абонента. Для него скорость изменения сигнала равна Sб(t) = drб(t)/dt. Это случайная функция времени, и ее можно охарактеризовать действующим значением (дисперсией) S2д.б. С вероятностью, превышающей 0,99, можно принять, что максимальное значение скорости для сильного абонента Snик.6 не превышает значения Sпикб = 3Sд.б. Действующее значение процесса Sб(t) можно определить, зная энергетический спектр этого процесса Gs.б(f), по формуле
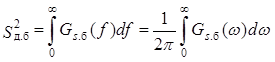 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.