Повышение эффективности канальных кодеков ЦСП. Классификация методов канального цифрового преобразования, страница 10

Поскольку , то энергетический спектр G_s.б(ω) можно выразить через энергетический спектр G_r.б(ω) сигнала r_б(t) следующим образом: G_s.б(ω) = G_r.б(ω)ω²  (см. параграф 2.10). Тогда

.                                     (14.26)

Выражение (14.26) является общим для произвольного спектра сигнала r(t). В качестве примера положим, что G_r.6(ω) = const = А в полосе частот ω  [ω_нс; ω_вс]. Тогда действующее значение сигнала r_б(t)равно

.

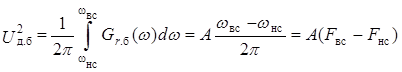Соответственно 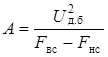 и на основании (14.26)

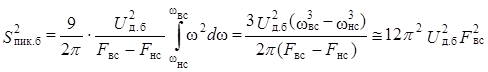.              (14.27)

В (14.27) для упрощения принято, что ω_вс>>ω_нс. Теперь, выражая ∆ из (14.24) и подставляя (14.27) в (14.25), получим

                     (14.28)

Как показывают экспериментальные исследования, реальные речеподобные сигналы имеют спектр, значительно отличающийся от равномерного, который принят в примере. Поэтому для них расчет по формуле (14.28) дает заниженный результат. Более высокую точность обеспечивает расчет ОСШК квантования, который основан на экспериментально проверенном утверждении, что реальный речеподобный сигнал r(t) c действующим значением U_димеет такое же значение ОСШК, что и синусоидальный сигнал с частотой f₀= 800 Гц и амплитудой U_m, равной пиковому значению сигнала r(t). Тогда полагаем

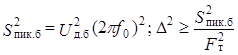
и на основании (14.25)

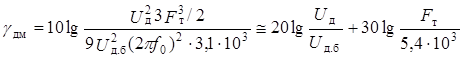.                  (14.29)

Сравним качественные показатели ДМ и ИКМ, используя (14.29) и формулу (12.16), которую удобно записать в виде

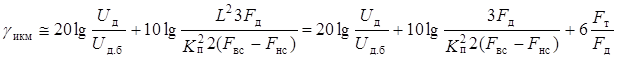.  (14.30)

Здесь F_т— тактовая частота цифрового сигнала, которая связана с частотой дискретизации F_дсоотношением F_т = F_д т, где т — число разрядов кодовой комбинации; при этом L = 2^m = 2^Fт/Fди соответственно l0 lgL² = 2(F_т / F_д)∙10 lg2.

При дельта-модуляции тактовая частота совпадает с частотой дискретизации. Оба вида модуляции можем сравнивать по величине ОСШК при одинаковых частотах импульсного потока F_Tили по частоте F_тпри одинаковых ОСШК. Если в качестве примера принять U_д = U_дм, что соответствует «слабому» абоненту, и положить γ_дм = γ_икм = 25 дБ, а также учесть, что 10 lg(U_дм/U_д.б) ≈ –30дБ, то тогда для ИКМ из (14.30) получим т≈ 11, F_т = 11 F_д= 88 кГц. Для ДМ на основании (14.29) имеем F_т= 5,40∙10³∙68 ≈ 370 кГц. Если же потребовать γ = 25 дБ при передаче сильного абонента, то тогда для ИКМ получим т = 6, F_т = 48 кГц, а для ДМ — F_т≈ 40 кГц.

Примерный график, позволяющий сравнить ДМ и ИКМ по ОСШК, изображен на рис. 14.16. Из него следует, что при малых величинах ОСШК дельта-модуляция позволяет использовать более низкую тактовую частоту, чем ИКМ; при больших значениях ОСШК преимущество имеет ИКМ. Указанное обстоятельство говорит, конечно, не в пользу ДМ, однако она имеет перед ИКМ ряд преимуществ, которые не позволяют сделать однозначный выбор сравниваемых систем. К достоинствам ДМ можно отнести следующие.

1.  ДМ менее чувствительна к искажениям в каналах связи, что позволяет работать с такими помехами, при которых ИКМ работать уже не может. Это обусловлено тем, что искажение любого символа в кодовой комбинации приводит к искажению всей комбинации, а затем и выборки, а при ДМ искажение отдельного символа вызывает искажение только приращения этой выборки, соответственно допустимый коэффициент ошибок в канале для ДМ не более 10^–3, тогда как для ИКМ — не более 10^–6 [11, 40, 49].

2.  При ИКМ необходимо обеспечить передачу сигналов синхронизации, с помощью которых определяется начало (конец) кодовых комбинаций; без них невозможна правильная работа декодера ИКМ. При ДМ указанный вид синхронизации не нужен.

3. Объединение нескольких цифровых источников при ДМ осуществляется более просто, чем при ИКМ.

4. Модулятор и демодулятор при ДМ проще конструктивно, что важно при построении абонентской цифровой сети.

Указанные преимущества ДМ обусловили дальнейшее развитие систем ДМ, направленное на снижение тактовой частоты при обеспечении приемлемой величины ОСШК. В настоящее время разработано большое число разновидностей систем ДМ, которые в основном являются адаптивными (АДМ).

14.3.2. Адаптивная ДМ