Повышение эффективности канальных кодеков ЦСП. Классификация методов канального цифрового преобразования, страница 4

При разрыве цепи обратной связи в кодере ДИКМ (см. рис. 14.2) вместо разностного сигнала y(t)передается исходный сигнал U(t), соответственно получим y_пик.б = U_пик.б = = K_пU_д.б. Тогда (14.9) трансформируется в (12.16) и характеризует ОСШ квантования в системе ИКМ. Если полагать, что для ИКМ и ДИКМ применяются одинаковые значения F_ди L, то «выигрыш» системы ДИКМ относительно ИКМ по шумам квантования в децибелах можно оценить величиной

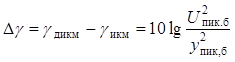.                                   (14.10)

Для максимизации выигрыша ∆γ необходимо, как следует из (14.7), (14.10), минимизировать величину σ_у.б. Используя (14.6), получим

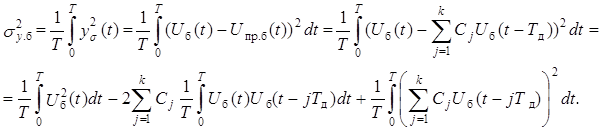.   (14.11)

Учтем в (14.11), что, по определению (см. параграф 1.3),

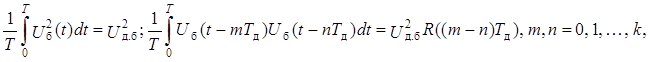 (14.12)

где R(рТ_д) = R(–pT_д) -- нормированный коэффициент корреляции сигнала U_б(t) в момент времени τ = рТ_д, р = 0, 1, 2,..., k, при этом всегда |R(pT_д)| < 1,0.

Тогда (14.11) приводится к виду

.                     (14.13)

Минимум σ_у.б обеспечивается при определенных (оптимальных) значениях коэффициентов предсказания С_j.opt которые находятся путем решения системы уравнений вида.

В качестве примера положим, что используется предсказание первого порядка: U_пр(t) = C₁U(t – Т_д). Тогда из (14.13) для k= 1 получим

 ,                                       (14.14)

откуда

C_1.opt = R(T_д);   σ²_y.б.min = U²_д.б(1 – R²(T_д)).                    (14.15)

Подставляя (14.14) в (14.10), оценим выигрыш ДИКМ при таком предсказании в децибелах:

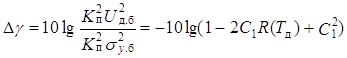.                   (14.16)

При C₁ = 1 и С₁ = С_1.орt, получаем соответственно

∆γ = –3 – 10 lg(1–R(T_д));  ∆γ_max = 10 lg(1–R²(T_д)).            (14.17)

Как следует из (14.16), (14.17), ДИКМ может обеспечить улучшение качественных показателей по сравнению с ИКМ, если на интервале Т_д сохраняется высокая корреляция между двумя соседними отсчетами: R(T_Д) → 1. При слабой корреляции (в частности, при С₁ = 1 и R(T_д) < 0,5) ∆γ < 0 и ДИКМ хуже ИКМ. Корреляция отсутствует, когда соседние отсчеты соответствуют разным каналам; следовательно, ДИКМ нецелесообразно применять по отношению к групповому АИМ-сигналу, полученному путем временного уплотнения. Если же использовать ДИКМ для кодирования индивидуальных сигналов, а затем применить временное уплотнение полученных кодовых комбинаций, то при таком построении ЦСП в каждом индивидуальном кодере ДИКМ обеспечивается высокая корреляция между отсчетами, а следовательно, и более высокое отношение сигнал—шум квантования. Этот выигрыш можно «обменять» на уменьшение числа уровней квантования Lи соответственно уменьшение тактовой частоты группового цифрового сигнала, что зачастую является решающим. Поскольку использование индивидуальных кодеров-декодеров ДИКМ приводит к усложнению оконечного оборудования, то ДИКМ применяется обычно в малоканальных системах или для передачи сравнительно малочисленных широкополосных сигналов типа звукового вещания, телевидения и видеотелефона.

Проиллюстрируем это положение некоторыми примерами. Так, при передаче типичного телефонного сигнала и частоте дискретизации F_д = 8 кГц (T_д = 125 мкс) имеем R(T_д) ≈ 0,8 [см. формулу (1.30)]. Тогда из (14.17) при C₁ = 1 получим ∆γ = 4 дБ. Из материалов параграфа 12.3 известно, что изменение длины двоичной кодовой комбинации на один разряд вызывает изменение отношения сигнал—шум квантования на 6 дБ. Следовательно, если выигрыш, полученный от использования ДИКМ вместо ИКМ, «обменять» на уменьшение длины кодовой комбинации на один разряд, в результате получим проигрыш в величине ОСШ квантования на 2 дБ, что, как правило, недопустимо.

При передаче сигналов звукового вещания, когда частота дискретизации выбирается порядка 32 кГц, коэффициент корреляции R(T_д = (32∙10³)^–1c) ≈ 0,98 и на основании (14.17) выигрыш ДИКМ составляет порядка 14 дБ. Такой выигрыш можно «обменять» на уменьшение кодовой комбинации (на два разряда) и соответственно понижение тактовой частоты цифрового сигнала звукового вещания.