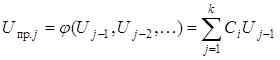Повышение эффективности канальных кодеков ЦСП. Классификация методов канального цифрового преобразования, страница 3

,                                    (14.6)

где k — число предыдущих отсчетов, учитываемых при таком линейном предсказании; С_i — коэффициенты влияния (j – i)-го отсчета на j-й.

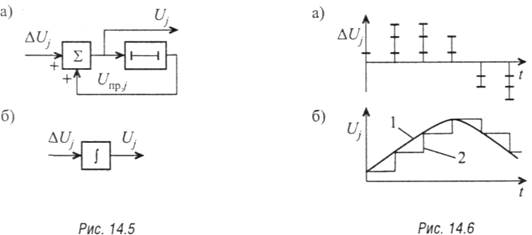
Приемная часть системы ДИКМ при предсказании первого порядка имеет вид, показанный на рис. 14.5, а. На рис. 14.5, б приведен аналог этой системы, выполненный на основе интегратора. Осциллограммы поясняют процессы в отдельных точках кодера (рис. 14.6, а) и декодера ДИКМ (рис. 14.6, б) с таким предсказателем. На рис. 14.6, а показаны квантованные отсчеты разностного сигнала, а на рис. 14.6, бсплошная кривая 1 соответствует входному сигналу, а ступенчатая 2 — предсказанному, полученному в цепи обратной связи. Аналогичный вид имеет восстановленный квантованный сигнал на выходе интегратора приемника.

Реализация кодера и декодера ДИКМ отличается построением предсказателя. При этом возможны два варианта: аналоговый и цифровой. Декодер ДИКМ с аналоговым предсказателем первого порядка упрощенно показан на рис. 14.7; временные диаграммы, иллюстрирующие его работу, представлены на рис. 14.8. Здесь используются два ключа S1 и S2, которые открываются в разные моменты времени (рис. 14.8, б, в), чтобы исключить самовозбуждение пред сказателя. Разностный квантованный сигнал (рис. 14.8, а), получаемый с выхода декодера 4 (см. рис. 14.1, 14.2), складывается с предсказанным сигналом, получаемым на накопительном конденсаторе С2. В момент t₁ (при включении S1) эта сумма сигналов заряжает промежуточный накопитель С1 (рис. 14.8, д). Затем ключ S1 отключается, разрывая цепь обратной связи, а в момент t₂ (при включении 52) происходит «дозаряд» накопителя С2 до напряжения, равного U_c1(рис. 14.8, г).

Цифровой вариант предсказателя ДИКМ представлен на рис. 14.9. Здесь цифровой разностный сигнал ∆N_j впараллельном k-разрядном коде поступает на первые входы цифровогосумматора 1. На вторые входы подается в параллельном коде л-разрядное число, соответствующее предсказанному значению N_nр.j (n > k). Это число хранилось в блоке буферной памяти 2. На выходе сумматора / образуется двоичное число N_j = N_np.j +∆N_j, которое в параллельном n-разрядном коде поступает в линейный ЦАП (блок эталонов) 3 и блок 2. На выходе ЦАП получается квантованный отсчет Uj, соответствующий числy N_j.

14.2.2. Помехозащищенность и оптимизация параметров

Как и в системах с ИКМ, при использовании ДИКМ возникают ошибки при восстановлении отсчетов (U'_j ≠ U_j), которые обусловлены двумя причинами:

а) квантованием разностного сигнала y(t) = ∆U(t) = U(t) – U_np(t);

б) ограничением сигнала y(t), когда его размах превышает пороги шкалы квантования кодера. Ограничение сигнала y(t) приводит к тому, что предсказанный сигнал U_np(t)не успевает «отслеживать» сигнал U(t). Возникающие при этом искажения восстановленного сигнала называют шумом перегрузки.

Действующее значение σ_у случайного сигнала y(t) для разных абонентов будет изменяться в интервале σ_у  [σ_у.м; σ_у.б], где, как и ранее, индекс «м» соответствует слабому (малому) абоненту, а индекс «б» — сильному (большому). Максимальное (пиковое) значение сигнала y(t) будет определяться самым сильным абонентом: У_пик.б = max[y_б(t)] = σ_y.бK_п, где К_п— пик-фактор разностного сигнала.

Положим сначала, что шумы ограничения отсутствуют, т.е. порог ограничения кодера выбран не менее у_пик.б. Если шкала квантования симметричная и равномерная, а число уровней квантования равно L, то, учитывая материалы параграфа 12.3, получаем:

шаг квантования

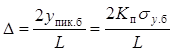,                                            (14.7)

мощность (дисперсия) шума квантования

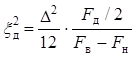,                                               (14.8)

отношение сигнал—шум квантования для произвольного абонента с действующим напряжением U_д [U_д.м; U_д.б]

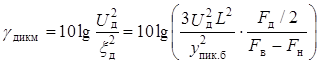.                             (14.9)