В цифровом телевидении обычно используется раздельное аналого-цифровое преобразование яркостных и цветоразностных компонентов сигнала. Яр-костная составляющая дискретизируется с частотой порядка 13,5 МГц, при этом коэффициент корреляции равен 0,99. Использование ДИКМ вместо ИКМ дает выигрыш порядка 20 дБ, а применение обменных соотношений позволяет на 3—4 разряда (относительно исходных 8—9 разрядов) уменьшить длину кодовой комбинации и соответственно почти в 2 раза уменьшить тактовую частоту цифрового сигнала.
Использование более сложных схем предсказателей (см. рис. 14.4) с оптимальными коэффициентами предсказания Cj.opt, j = 2, 3, … и т.д. позволяет получить дополнительный выигрыш в помехозащищенности порядка 4—6 дБ (при К(Тд) > 0,98). На практике они применяются только в телевизионных кодеках или в адаптивных речевых кодеках.
Дальнейшее повышение эффективности ДИКМ применительно к указанным выше сигналам реализуется за счет использования неравномерных и (или) адаптивных шкал квантования, обеспечивающих тот или иной способ компрессии динамического диапазона сигнала. Здесь, как и для систем с ИКМ, может быть определен оптимальный закон компрессии, который зависит от статистических характеристик отдельного абонента, и квазиоптимальный, который почти инвариантен к разбросу уровней абонентов. В последнем случае применяют известные квазилогарифмические законы компрессии типа А или μ (см. параграф 13.3). Они реализуются с помощью нелинейных функциональных или (чаше) цифровых преобразователей, причем возможно осуществление компрессии по разностному или по предсказанному сигналу. Первый вариант (назовем его АДИКМ-1) показан на рис. 14.3. Здесь в нелинейном декодере разностного сигнала, включенном в цепь обратной связи кодера ДИКМ, используется экспандер на основе НЦП 6.
Расчет характеристик системы АДИКМ-1 с нелинейной шкалой квантования производится по такой же методике и формулам, что и для ИКМ (см. параграф 13.4), при этом вместо исходного сигнала U(t), который имеет действующее напряжение Uд и определенную плотность распределения мгновенных значений W(U), подставляется разностный сигнал y(i). Для него действующее значение σу определяется из (14.13)—(14.17), а плотность распределения мгновенных значений W(y) принимается равной
.
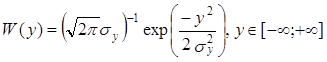(14.18)
Выражение (14.18) соответствует нормальному (Гауссову) закону распределения с нулевым математическим ожиданием (средним значением). Такой выбор оправдан тем, что y(t) определяется из (14.1), (14.6), т.е. равен сумме (разности) нескольких случайных величин, следовательно, в значительной степени удовлетворяет предельной теореме Чебышева: случайная величина, равная сумме (разности) большого числа случайных величин, которые имеют произвольное распределение, подчиняется нормальному закону распределения.
При выборе кусочно-линейных шкал квантования (по А- или μ-законам) шумы квантования и ограничения при АДИКМ-1 рассчитываются по методике параграфа 13.4 (за исключением формул (13.31), (13.32)). Вместо них при подстановке (14.18) получим соответственно
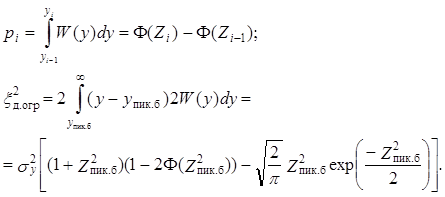(14.19)
.
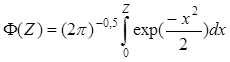(14.20)
Здесь Zi = yi / σi; Zпик.б = yпик.б / σy; yi — верхняя граница i-го сегмента шкалы квантования; упик.б — пороговое значение шкалы (верхняя граница последнего сегмента); таблица значений Ф(z) приведена в работах [5, 38].
Расчет защищенности от шумов квантования и ограничения производится на основании (13.27), (13.39) и (14.20), при этом вместо (13.31) подставляется (14.19), а в выражениях (13.30) вместо величины Uм = Uпик.б берется упик.6. Величина σу в (14.20) рассчитывается на основании (14.13), а при использовании предсказания первого порядка — из (14.14).
В качестве примера на рис. 14.10 приведены рассчитанные нами (см. [31]) по указанным формулам зависимости защищенности от шумов квантования и ограничения γадикм.1 в случае фиксированного предсказания первого порядка (графики 1—8).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.