Повышение эффективности канальных кодеков ЦСП. Классификация методов канального цифрового преобразования, страница 12

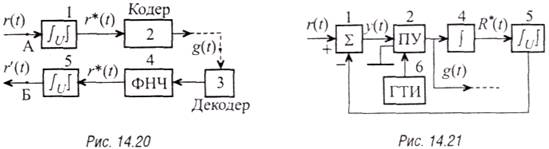
Простейший вариант адаптивной ДМ с инерционной компрессией (рис. 14.20) реализуется за счет введения на передающей стороне компрессора 7, а на приемной — экспандера 5. Основные блоки — кодер 2, декодер 3 и ФНЧ 4 — образуют классическую (линейную) систему ДМ. Аналоговые компрессор 1 и экспандер 5 (совместно — компандер) собраны по типовым схемам (см. параграф 9.6) с инерционным (слоговым) управлением по аналоговому компрессированному сигналу r*(t). Необходимость обеспечения равномерной сквозной амплитудной характеристики системы (между точками А и Б на рис. 14.20) не позволяет выполнить компрессию сигнала в широких пределах (сложно создать блоки 1 и 5 со взаимно обратными характеристиками), поэтому существенно улучшить показатели АДМ для этого варианта не удается.

Значительно проще обеспечить глубокую компрессию динамического диапазона, если нелинейный кодер (совокупность блоков 1 и 2 на рис. 14.20) реализовать по схеме «кодер с нелинейным декодером (совокупность блоков 3, 4, 5 на рис. 14.20) в цепи обратной связи» (рис. 14.21). Здесь на стороне передачи и приема используют однотипный экспандер 5, остальные блоки пояснялись ранее. Экспандер управляется аналоговым квантованным сигналом R*(t) по типовой схеме инерционного управления (см. параграф 9.6).

Более высокие качественные показатели обеспечивают варианты АДМ с управлением по цифровому сигналу g(t). Если кодер и декодер ДМ выполнены на основе цифровой схемотехники (рис. 14.22), то компрессию можно обеспечить с помощью нелинейного цифрового преобразователя (НЦП), имеющего кусочно-линейную характеристику экспандирования (см. подпараграф 13.3.4). Здесь цифровой сигнат кодера g(t), представляющий собой последовательность символов 0 и 1. поступает на вход реверсивного счетчика (PC) 4. При поступлении символа 1 число, записанное в PC, увеличивается на единицу, при поступлении 0 — уменьшается на 1. Следовательно, PC выполняет функцию цифрового интегратора. На его выходе образуется q-разрядное число в параллельном коде, которое поступает в НЦП 5. С выхода НЦП р-разрядное число (р > q) подается в ЦАП (блок эталонов) 6, где формируется квантованный сигнал предсказания U_пр(t) = R(t), который поступает в аналоговую схему вычитания 1. Декодер системы состоит из аналогичных блоков 7—9. Назначение генераторов тактовых импульсов 3 и 10, порогового устройства 2 и ФНЧ 11 не требует пояснений.

Процесс слежения в такой адаптивной системе отличается тем, что изменение цифрового сигнала g(t) на единицу вызывает изменение предсказанного сигнала R(t) на величину ∆R, которая меняется в зависимости от текущего значения R(t):величина ∆R максимальна, когда R(t) находится в пределах старшего сегмента характеристики НЦП (см. рис. 13.55), и ∆R минимальна, когда R(t) соответствует младшему сегменту. Другими словами, в такой системе слежение осуществляется с разным шагом ∆_i. По аналогии с материалом параграфа 13.4 дисперсия шумов квантования будет равна

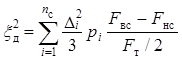,                                            (14.31)

где p_i — вероятность попадания мгновенного значения сигнала R(t) в интервал [U_i–1;U_i]i-го сегмента; i  [1, п_с]; п_с — число сегментов характеристики НЦП; ∆_i — шаг слежения в пределах i-го сегмента.

Для кусочно-линейных законов компрессии имеем:

A-закон: ∆₁ = ∆₂ = 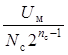; ∆_i= ∆₂2^i-2, 2 ≤ i ≤ n_c;

μ-закон: ∆₁=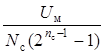; ∆_i = ∆₁2^i-1, 1 ≤ i ≤ n_c;

где N_c— число шагов в пределах сегмента; U_м — максимальное значение шкалы квантования ЦАП, включенного на выходе НЦП (см. рис. 14.22).

При этом самый большой шаг квантования ∆_mах (для i = n_с) отличается от самого малого ∆_min (i = 1) соответственно в 2^nс–2 или 2^nc–1 раз. Значения р_i для речеподобного сигнала с действующим значением U_д определяются из (13.31). Если плотность распределения сигнала соответствует нормальному закону, то можно использовать выражения (14.19)—(14.21), приняв Z_i = U_i/U_д, Z_пик.б = U_пик.д/U_д. Пороговое значение характеристики НЦП соответствует пиковому напряжению самого сильного абонента U_пик.б = U_м,чтобы не было шумов ограничения.